题目内容
2.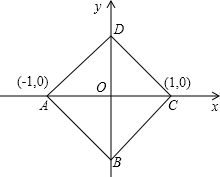 已知如图,点A(-1,0)、C(1,0),以AC为对角线作正方形ABCD.
已知如图,点A(-1,0)、C(1,0),以AC为对角线作正方形ABCD.(1)写出点B,点D的坐标;
(2)用直尺或圆规作出:y轴上分别到点B、点D的距离等于正方形边长的点(简要说明作法并保留作图痕迹);
(3)已知直线l:y=x+m,点P为直线l上的动点,当直线l上存在唯一一个点P使得∠APC=45°时,求m的值.
分析 (1)根据正方形的对角线互相垂直平分且相等即可求得;
(2)分别以D和B为圆心,正方形的边长为半径作弧,与y轴的交点就是满足条件的点;
(3)当直线l上存在唯一一个点P使得∠APC=45°时,直线与分别以B和D为圆心,有AB的圆为半径的圆相切,据此即可求解.
解答 解:(1)B的坐标是(0,-1),D的坐标是(0,1);
(2)分别以D和B为圆心,正方形的边长为半径作弧,与y轴的交点就是满足条件的点.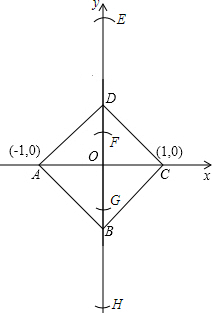
点E、F、G、H是所求的点;
(3)当直线y=x+m经过第二、一、三象限时,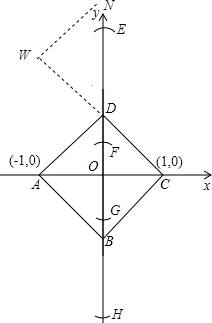
过D作直线y=x+m的垂线,当直线l上存在唯一一个点P使得∠APC=45°时,DW=AB=$\sqrt{2}$,
直线y=x+m与y轴的交点是N,则△DWN是等腰直角三角形,则DN=$\sqrt{2}$DW=2,
则ON=OD+DN=1+2=3,即N的坐标是(0,3).
把(0,3)代入y=x+m得m=3,
则函数解析式是y=x+3;
同理,当直线y=x+m经过第一、四、三象限时,函数解析式是y=x-3.
点评 本题考查了正方形的性质,以及待定系数法求解析式,理解:当直线l上存在唯一一个点P使得∠APC=45°时,直线与分别以B和D为圆心,有AB的圆为半径的圆相切是关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
10.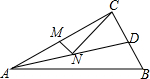 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
 如图,在△ABC中,∠A=70°,∠ABC=60°,CD平分∠ACB,BE为AC边上的高,求∠BOC的度数.
如图,在△ABC中,∠A=70°,∠ABC=60°,CD平分∠ACB,BE为AC边上的高,求∠BOC的度数.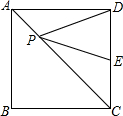 正方形ABCD中,点P是对角线AC上的动点,点E是CD的中点,AB=2,求PD+PE的最小值.
正方形ABCD中,点P是对角线AC上的动点,点E是CD的中点,AB=2,求PD+PE的最小值. 如图是一个三角形数阵,根据该数阵的规律,猜想第八行所有数的和是512.
如图是一个三角形数阵,根据该数阵的规律,猜想第八行所有数的和是512.