题目内容
1.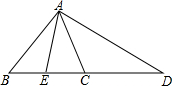 如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.
如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.
分析 首先延长AE至M,使EM=AE,先证明△ABE≌△MCE,进而得出MC=AB,AE=EM,AD=2AE,得出AD=AM,AC平∠EAD,得出∠MAC=∠DAC,再证明△ACM≌△ACD,即可得出答案.
解答 证明:如图,
延长AE至M,使EM=AE,
在△ABE和△MEC中,
$\left\{\begin{array}{l}{BE=CE}\\{∠AEB=∠MEC}\\{AE=ME}\end{array}\right.$,
∴△ABE≌△MCE(SAS),
∴MC=AB,AE=EM,
∵AD=2AE,
∴AD=AM,
∵AC平∠EAD,
∴∠MAC=∠DAC,
在△ACM和△ACD中,
$\left\{\begin{array}{l}{AC=AC}\\{∠MAC=∠DAC}\\{AM=AD}\end{array}\right.$,
∴△ACM≌△ACD(SAS).
∴CM=CD,
∴AB=CD.
点评 此题主要考查了全等三角形的判定与性质,利用倍长中线得出辅助线是解题关键.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
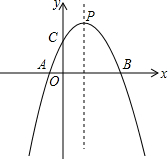 如图,抛物线y=-x2+bx+c的对称轴是直线x=1,与y轴交于点C(0,3),与x轴交于 A,B两点.
如图,抛物线y=-x2+bx+c的对称轴是直线x=1,与y轴交于点C(0,3),与x轴交于 A,B两点.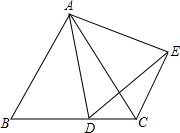 已知△ABC为等边三角形,D为BC边上一点,△ADE也是等边三角形
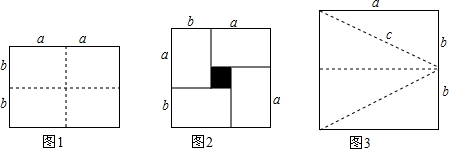
已知△ABC为等边三角形,D为BC边上一点,△ADE也是等边三角形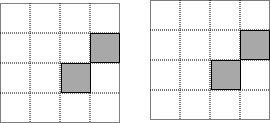 由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图).请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图).请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑,使它成为轴对称图形. 如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=5或10,△ABC与△APQ全等.
如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=5或10,△ABC与△APQ全等.