如图所示.AB是圆O的直径.以OA为直径的圆C与圆O的弦AD相交于点E．求证:点E为AD的中点．题目和参考答案——青夏教育精英家教网——

题目内容

2．

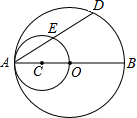如图所示，AB是圆O的直径，以OA为直径的圆C与圆O的弦AD相交于点E．
求证：点E为AD的中点．

分析连接OE，由于OA为⊙C的直径，得到∠AEO=90°，即OE⊥AD，在⊙0中，根据垂径定理可得EA=EB．

解答证明：∵AO是⊙C的直径，
∴∠AEO=90°，即OE⊥AD于E，
又∵OE经过圆心O，
∴AE=DE，
即：点E为AD的中点．

点评本题考查了圆周角定理的推论：直径所对的圆周角为直角；也考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．

练习册系列答案

全优课时作业系列答案

英才计划赢在起跑线系列答案

巧思妙算系列答案

全优训练期末测试卷系列答案

新课程成长资源系列答案

新课堂单元测试卷冲刺100分系列答案

学业测评期末考试真题汇编系列答案

名校特优卷系列答案

名校名卷期末冲刺100分系列答案

应用题天天练南海出版公司系列答案

相关题目

12．（1）如图1：一个长方形长为2a，宽为2b，若把此图沿图中虚线用剪刀均分为四块小长方形，然后按图2的形状拼成一个大正方形，中间围成一个小正方形（图中阴影部分），请将图2中阴影部分的面积用含a、b的代数式表示出来：（a-b）²，并根据图2面积，写出一个等式：（a+b）²=（a-b）²+4ab
（2）如图3，一个长方形长为a，宽为2b，若把此图沿图中虚线用剪刀均分为四块小直角三角形（斜边为c），然后拼成一个正方形，中间围成一个小正方形．
①请画出围成的示意图（按图3所给尺寸大小）
②根据你所画的图形面积写出一个等式，并探究直角三角形三边a、b、c具有怎样的数量关系，用文字语言表述出来．

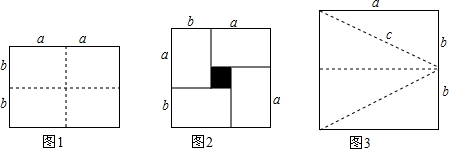
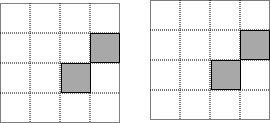由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑（如图）．请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑，使它成为轴对称图形．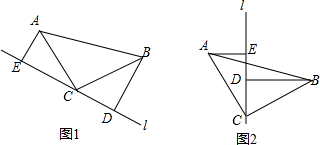

10．计算．
（1）7-（-2）+（-3）．
（2）$（-\frac{3}{7}）+\frac{5}{6}-（-2\frac{1}{7}）+（-\frac{5}{6}）$
（3）$16÷{（-2）^3}-\frac{1}{6}×（-3）$
（4）（-81）÷$\frac{9}{4}×\frac{4}{9}$÷（-16）
（5）（$\frac{1}{2}-\frac{5}{9}+\frac{7}{12}$）×（-36）
（6）$1\frac{1}{2}$×$\frac{5}{7}-（-\frac{5}{7}）$×$2\frac{1}{2}$+（-$\frac{1}{2}$）$÷1\frac{2}{5}$．

17．如图，△ABC中，∠ACB=90°，AC=BC，直线l过点C，BD⊥l，AE⊥l，垂足分别为D、E．
（1）当直线l不与底边AB相交时，求证：ED=AE+BD；
（2）如图2，将直线l绕点C顺时针旋转，使l与底边AB相交时，请你探究ED、AE、BD三者之间的数量关系．

7．计算：
①（-5.2）-（+4.8）+（-3.2）-（-2.3）
②$（-\frac{3}{7}）+\frac{5}{6}-（-2\frac{1}{7}）+（-\frac{5}{6}）$
③-2$\frac{1}{3}$×（-1$\frac{1}{6}$）÷（-7）×$\frac{1}{7}$
④-1⁴-（1-0.5）×$\frac{1}{3}×$[2-（-3）²]．

把两根钢条A′B、AB′的中点连在一起，可以做成一个测量工件内槽宽工具（卡钳）．如图，若测得AB=5厘米，则槽为5厘米．

如图，∠C=90°，AC=10，BC=5，AX⊥AC，点P和点Q从A点出发，分别在线段AC和射线AX上运动，且AB=PQ，当点P运动到AP=5或10，△ABC与△APQ全等．

12．已知线段AB，点C是它的黄金分割点（AC＞BC）．设以AC为边的正方形的面积为S₁，以AB、CB分别为长和宽的矩形的面积为S₂，则S₁与S₂关系正确的是（　　）