题目内容

18．已知点A（-6，y1），B（-3，y2），C（3，y3）都在函数y=（x+2）2+m的图象上，则（　　）
A．y1＜y2＜y3B．y3＜y2＜y1C．y3＜y1＜y2D．y2＜y1＜y3

分析 根据函数解析式的特点，其对称轴为x=-2，图象开口向上；利用对称轴左侧y随x的增大而减小，可判断y2＜y1，根据二次函数图象的对称性可判断y2＜y1＜y3．

解答 解：∵二次函数y=（x+2）2+m中a=1＞0，
∴抛物线开口向上．
∵x=-2，-6＜-3＜-2＜3，
∴A（-6，y1），B（-3，y2）在对称轴的左侧，且y随x的增大而减小，
∴y1＞y2．
∵由二次函数图象的对称性可知y2＜y1＜y3．
故选D．

点评 本题考查的是二次函数图象上点的坐标特点，熟知二次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．

练习册系列答案
相关题目
8．已知四个命题：
①若一个数的相反数等于它本身，则这个数是0；
②若一个数的倒数等于它本身，则这个数是1；
③若a=b，则a2=b2；
④若一个数的绝对值就等于它本身，则这个数是正数．
其中真命题有（　　）
A．1个B．2个C．3个D．4个
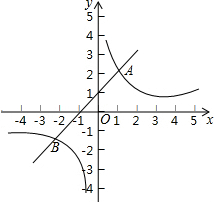9．如图，直线y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点 A（1，2）、B（-2，-1），则当取-2＜x＜0或x＞1时，$\frac{m}{x}$＜kx+b．
6．判断下列命题是真命题还有假命题．如果是真命题，请证明，如果是假命题，请举出反例．
（1）两个锐角的和是钝角；
（2）在同一平面内，垂直于同一条直线的两条直线互相平行．
13．因式分解：
（1）4x2-64y2；
（2）a2+b2+4a-4b-2ab+4．
3．阅读下面材料，并解答下列各题：
在形如ab=N的式子中，我们已经研究过两种情况：
①已知a和b，求N，这是乘方运算；
②已知b和N，求a，这是开方运算；
现在我们研究第三种情况：已知a和N，求b，我们把这种运算叫做对数运算．
定义：如果ab=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记着b=logaN．
例如：因为23=8，所以log28=3；因为2-3=$\frac{1}{8}$，所以log2$\frac{1}{8}$=-3．
（1）根据定义计算：
①log381=4；②log33=1；③log31=0；
④如果logx16=4，那么x=2．
（2）设ax=M，ay=N，则logaM=x，logaN=y（a＞0，a≠1，M、N均为正数），
∵ax•ay=ax+y，∴ax+y=M•N∴logaMN=x+y，
即logaMN=logaM+logaN
这是对数运算的重要性质之一，进一步，我们还可以得出：
logaM1M2M3…Mn=logaM1+logaM2+logaM3+…+logaMn（其中M1、M2、M3、…、Mn均为正数，a＞0，a≠1）
loga$\frac{M}{N}$=logaM-logaN（a＞0，a≠1，M、N均为正数）．仿照上面说明方法，任选一空试说明理由．
10．（1）$\sqrt{27}-\sqrt{\frac{1}{3}}+\sqrt{12}$　  
（2）$（{\sqrt{7}+\sqrt{3}}）（{\sqrt{7}-\sqrt{3}}）-\sqrt{16}$
（3）$\frac{{\sqrt{20}+\sqrt{5}}}{{\sqrt{45}}}-\sqrt{\frac{1}{3}}•\sqrt{6}$
（4）${（{2-\sqrt{10}}）^2}+\sqrt{40}$．
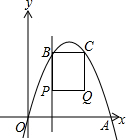7．如图，在平面直角坐标系中，经过原点的抛物线y=-x2+4mx（m＞0）与x轴的另一个交点为点A，过点P（1，m）作直线PB⊥x轴，交抛物线于点B，作点B关于抛物线对称轴的对称点C（点B、C不重合），连结BC，当点P、B不重合时，以BP、BC为边作矩形PBCQ，设矩形PBCQ的周长为l．
（1）当m=1时，求点A的坐标．
（2）当BC=$\frac{1}{2}$时，求这条抛物线所对应的函数表达式．
（3）当点P在点B下方时，求l与m之间的函数关系．
（4）连结CP，以CP为直角边作等腰直角三角形PCM，直接写出点M落在坐标轴上时m的值．
8．如图，在△ABC中，∠CAB=90°，AB=6，AC=4，CD是△ABC的中线，将△ABC沿直线CD翻折，点B′是点B的对应点，点E是线段CD上的点，如果∠CAE=∠BAB′，那么CE的长是$\frac{16}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网