题目内容
10.(1)$\sqrt{27}-\sqrt{\frac{1}{3}}+\sqrt{12}$(2)$({\sqrt{7}+\sqrt{3}})({\sqrt{7}-\sqrt{3}})-\sqrt{16}$
(3)$\frac{{\sqrt{20}+\sqrt{5}}}{{\sqrt{45}}}-\sqrt{\frac{1}{3}}•\sqrt{6}$
(4)${({2-\sqrt{10}})^2}+\sqrt{40}$.
分析 (1)先对原式化简,再合并同类项即可解答本题;
(2)根据平方差公式和算术平方根先对原式化简,再合并同类项即可解答本题;
(3)先对原式化简,再合并同类项即可解答本题;
(4)根据完全平方差和算术平方根可以对原式化简.
解答 解:(1)$\sqrt{27}-\sqrt{\frac{1}{3}}+\sqrt{12}$
=$3\sqrt{3}-\frac{\sqrt{3}}{3}+2\sqrt{3}$
=$\frac{2\sqrt{3}}{3}$;
(2)$({\sqrt{7}+\sqrt{3}})({\sqrt{7}-\sqrt{3}})-\sqrt{16}$
=7-3-4
=0;
(3)$\frac{{\sqrt{20}+\sqrt{5}}}{{\sqrt{45}}}-\sqrt{\frac{1}{3}}•\sqrt{6}$
=$\frac{2\sqrt{5}+\sqrt{5}}{3\sqrt{5}}-\sqrt{2}$
=$1-\sqrt{2}$;
(4)${({2-\sqrt{10}})^2}+\sqrt{40}$
=$4-4\sqrt{10}+10+2\sqrt{10}$
=14-2$\sqrt{10}$.
点评 本题考查二次根式的混合运算,解题的关键是明确二次根式的混合运算的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知2x=3y(xy≠0),则下列各式中错误的是( )
| A. | $\frac{x+y}{y}$=$\frac{5}{2}$ | B. | $\frac{x}{y}$=$\frac{2}{3}$ | C. | $\frac{x-y}{x+y}$=$\frac{1}{5}$ | D. | y=$\frac{2}{3}$x |
1.若频率为0.3,总数为100,则频数为( )
| A. | 0.3 | B. | 100 | C. | 30 | D. | 300 |
18.已知点A(-6,y1),B(-3,y2),C(3,y3)都在函数y=(x+2)2+m的图象上,则( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
5.长度为1cm、2cm、3cm、4cm、5cm的五条线段,若以其中的三条线段为边构成三角形,可以构成不同的三角形共有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
11.下列命题中,真命题的是( )
| A. | 两个锐角的和为直角 | B. | 两个锐角的和为钝角 | ||
| C. | 两个锐角的和为锐角 | D. | 互余且非零度的两个角都是锐角 |

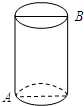 如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为多少cm(π取3.0).
如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为多少cm(π取3.0).