题目内容

9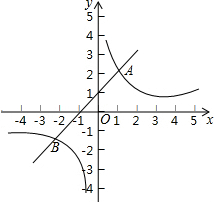．如图，直线y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于点 A（1，2）、B（-2，-1），则当取-2＜x＜0或x＞1时，$\frac{m}{x}$＜kx+b．

分析 根据函数图象可以明确x＜-2，-2＜x＜0，0＜x＜1，x＞1时直线y=kx+b与反比例函数y=$\frac{m}{x}$对应的函数值的大小，从而可以解答本题．

解答 解：由图象可知，当x＜-2时，$\frac{m}{x}$＞kx+b，
当-2＜x＜0时，$\frac{m}{x}$＜kx+b，
当0＜x＜1时，$\frac{m}{x}$＞kx+b，
当x＞1时，$\frac{m}{x}$＜kx+b．
故答案为：-2＜x＜0或x＞1．

点评 本题考查反比例函数与一次函数的交点问题、不等式，解题的关键是明确题意，利用数形结合的思想解答问题．

练习册系列答案
相关题目
19．计算：x3×（-x2）=-x5．
20．已知2x=3y（xy≠0），则下列各式中错误的是（　　）
A．$\frac{x+y}{y}$=$\frac{5}{2}$B．$\frac{x}{y}$=$\frac{2}{3}$C．$\frac{x-y}{x+y}$=$\frac{1}{5}$D．y=$\frac{2}{3}$x
17．如图，直线AB、CD相交于点O，∠DOE=∠BOD，OF平分∠AOE，∠BOD=20°．
（1）求∠AOE的度数；
（2）求∠COF的度数．
4．已知关于x，y的方程组$\left\{{\begin{array}{l}{ax+by=10}\\{mx-ny=8}\end{array}}\right.$的解是$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$，则关于x，y的方程组$\left\{{\begin{array}{l}{\frac{1}{2}a（x+y）+\frac{1}{3}b（x-y）=10}\\{\frac{1}{2}m（x+y）-\frac{1}{3}n（x-y）=8}\end{array}}\right.$的解为（　　）
A．$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$B．$\left\{{\begin{array}{l}{x=2}\\{y=1}\end{array}}\right.$C．$\left\{{\begin{array}{l}{x=4}\\{y=-2}\end{array}}\right.$D．$\left\{{\begin{array}{l}{x=3}\\{y=2}\end{array}}\right.$
14．若菱形两条对角线的长分别为12cm和16cm，则这个菱形的周长为（　　）
A．10cmB．20cmC．28cmD．40cm
1．若频率为0.3，总数为100，则频数为（　　）
A．0.3B．100C．30D．300
18．已知点A（-6，y1），B（-3，y2），C（3，y3）都在函数y=（x+2）2+m的图象上，则（　　）
A．y1＜y2＜y3B．y3＜y2＜y1C．y3＜y1＜y2D．y2＜y1＜y3
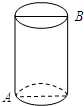19．如图所示，有一个圆柱体，高为12cm，底面半径为3cm，在圆柱下底面A处有一只蜘蛛．它想到上底面B处捉住一只苍蝇，则蜘蛛所走的最短路线长应为多少cm（π取3.0）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网