题目内容
16.过边长为2的正方形的中心O引两条相互垂直的射钱,分別与正方形的边交于A,B两点,则线段AB的长可能为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{2}$ |
分析 先证明△AOE≌△DOF,进而得到OE=OF,此为解决该题的关键性结论;求出OE的范围,借助勾股定理即可解决问题.
解答 解:如图所示: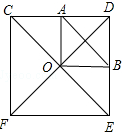
∵四边形CDEF是正方形,
∴∠OCD=∠ODB=45°,∠COD=90°,OC=OD,
∵AO⊥OB,
∴∠AOB=90°,
∴∠COA+∠AOD=90°,∠AOD+∠DOB=90°,
∴∠COA=∠DOB,
在△COA和△DOB中,$\left\{\begin{array}{l}{∠OCA=∠ODB}\\{OC=OD}\\{∠AOC=∠DOB}\end{array}\right.$,
∴△COA≌△DOB(ASA),
∴OA=OB,
设OA=OB=a,
∵∠AOB=90°,
∴△AOB是等腰直角三角形,
由勾股定理得:AB2=OA2+OB2=2a2,
由题意可得:1≤a≤$\sqrt{2}$,
∴$\sqrt{2}$≤AB≤2,
∵$\sqrt{2}$>1,$\sqrt{5}$>2,2$\sqrt{2}$>2,都不合题意,
只有$\sqrt{2}$<$\sqrt{3}$<2,符合题意.故选B.
点评 该题以正方形为载体,主要考查了正方形的性质、全等三角形的判定与性质等几何知识点的应用问题;牢固掌握全等三角形的判定等几何知识点,是灵活解题的基础和关键.

练习册系列答案
相关题目
7.已知二次函数y=ax2+bx-3图象的开口向上,对称轴在y轴右侧,则一次函数y=ax+b的图象不经过的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.等腰三角形一腰上的高与另一腰的夹角为20°,则底角的度数为( )
| A. | 55° | B. | 50° | C. | 50°或40° | D. | 35°或55° |
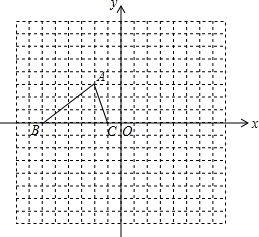 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0). 张明同学把一张长方形纸条ABCD按照如图那样沿线段OG折叠后量得∠AOE=58°,则∠EOG的度数是61°.
张明同学把一张长方形纸条ABCD按照如图那样沿线段OG折叠后量得∠AOE=58°,则∠EOG的度数是61°.