题目内容
6.在半径为5的圆中,60°的圆心角所对的扇形的面积为$\frac{25}{6}π$(结果保留π)分析 直接利用扇形面积公式计算即可.
解答 解:扇形的面积为:$\frac{60π×{5}^{2}}{360}$=$\frac{25}{6}π$,
故答案为:$\frac{25}{6}π$.
点评 此题主要考查了扇形的面积公式:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=$\frac{nπ{R}^{2}}{360}$.熟记公式是解题的关键.

练习册系列答案
相关题目
16. 如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )
如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )
 如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )
如图,四个有理数在数轴上的对应点分别为M,P,N,Q,若原点在点N与点P之间,则绝对值最大的数表示的点是( )| A. | 点M | B. | 点P | C. | 点Q | D. | 点N |
14.下列各项是同类项的是( )
| A. | 5与6 | B. | (a2)3与a5 | C. | 2a3与3a2 | D. | $\frac{1}{2}$m2n与-n2m |
11.-0.2的倒数是( )
| A. | 0.2 | B. | -2 | C. | -$\frac{1}{5}$ | D. | -5 |
18. 某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示该电路中电流I与电阻R的函数关系图象.则该电路中某导体电阻为4(Ω),导体内通过的电流为( )
某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示该电路中电流I与电阻R的函数关系图象.则该电路中某导体电阻为4(Ω),导体内通过的电流为( )
 某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示该电路中电流I与电阻R的函数关系图象.则该电路中某导体电阻为4(Ω),导体内通过的电流为( )
某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示该电路中电流I与电阻R的函数关系图象.则该电路中某导体电阻为4(Ω),导体内通过的电流为( )| A. | 1.5(A) | B. | 6(A) | C. | $\frac{2}{3}$(A) | D. | 4(A) |
16.过边长为2的正方形的中心O引两条相互垂直的射钱,分別与正方形的边交于A,B两点,则线段AB的长可能为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{2}$ |
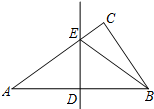 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=10,AC=8,则△BCE的周长是14.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=10,AC=8,则△BCE的周长是14. 如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=2$\sqrt{3}$,BE=1.
如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=2$\sqrt{3}$,BE=1.