题目内容
5.等腰三角形一腰上的高与另一腰的夹角为20°,则底角的度数为( )| A. | 55° | B. | 50° | C. | 50°或40° | D. | 35°或55° |
分析 根据等腰三角形的性质及三角形内角和定理进行分析,注意分类讨论思想的运用.
解答 
 解:①∵AB=AC,∠ABD=20°,BD⊥AC,
解:①∵AB=AC,∠ABD=20°,BD⊥AC,
∴∠A=70°,
∴∠ABC=∠C=(180°-70°)÷2=55°.
②∵AB=AC,∠ABD=20°,BD⊥AC,
∴∠BAC=20°+90°=110°
∴∠ABC=∠C=(180°-110°)÷2=35°.
故选D.
点评 此题主要考查三角形内角和定理及三角形外角的性质的综合运用,熟练掌握这两个定理是解决问题的关键.

练习册系列答案
相关题目
16.过边长为2的正方形的中心O引两条相互垂直的射钱,分別与正方形的边交于A,B两点,则线段AB的长可能为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{2}$ |
20.分式$\frac{3x}{x-2}$有意义,则x的取值范围是( )
| A. | x>2 | B. | x≠2 | C. | x=2 | D. | x≠0 |
17.某果园第1年水果产量为100吨,第3年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
| A. | 144(1-x)2=100 | B. | 100(1-x)2=144 | C. | 144(1+x)2=100 | D. | 100(1+x)2=144 |
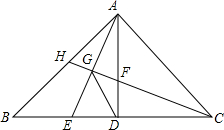 如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.
如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,点E是线段BD上一点,连接AE,CH⊥AE交AD于F,交AE于G,交AB于H,连接GD.