题目内容
7.已知二次函数y=ax2+bx-3图象的开口向上,对称轴在y轴右侧,则一次函数y=ax+b的图象不经过的象限为( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 首先根据二次函数y=ax2-bx图象的开口向上且对称轴在y轴的右侧确定a、b的符号,然后确定直线y=ax-b经过的象限.
解答 解:∵二次函数y=ax2+bx-3图象的开口向上,对称轴在y轴的右侧,
∴a>0,b<0,
∴直线y=ax+b不经过的第二象限,
故选B.
点评 考查了二次函数的性质以及一次函数图象和系数的关系,在直线y=kx+b中,当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.

练习册系列答案
相关题目
18. 某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示该电路中电流I与电阻R的函数关系图象.则该电路中某导体电阻为4(Ω),导体内通过的电流为( )
某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示该电路中电流I与电阻R的函数关系图象.则该电路中某导体电阻为4(Ω),导体内通过的电流为( )
 某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示该电路中电流I与电阻R的函数关系图象.则该电路中某导体电阻为4(Ω),导体内通过的电流为( )
某闭合电路中,电源电压为定值,电流I(A)与电阻R(Ω)成反比例,如图表示该电路中电流I与电阻R的函数关系图象.则该电路中某导体电阻为4(Ω),导体内通过的电流为( )| A. | 1.5(A) | B. | 6(A) | C. | $\frac{2}{3}$(A) | D. | 4(A) |
2.截至2013年末全国大陆总人口约为1360000000人,数字1360000000用科学记数法表示为( )
| A. | 136×107 | B. | 13.6×108 | C. | 1.36×109 | D. | 0.136×1010 |
19.九张同样的卡片分别写有数字-4,-3,-2,-1,0,1,2,3,4,任意抽取一张,所抽卡片上数字的绝对值不大于3的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{7}{9}$ |
16.过边长为2的正方形的中心O引两条相互垂直的射钱,分別与正方形的边交于A,B两点,则线段AB的长可能为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{2}$ |
17.某果园第1年水果产量为100吨,第3年水果产量为144吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
| A. | 144(1-x)2=100 | B. | 100(1-x)2=144 | C. | 144(1+x)2=100 | D. | 100(1+x)2=144 |
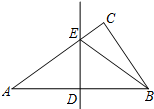 如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=10,AC=8,则△BCE的周长是14.
如图,在Rt△ABC中,∠ACB=90°,DE是AB的中垂线,分别交AB,AC于点D,E.已知AB=10,AC=8,则△BCE的周长是14.