题目内容
20.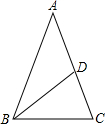 如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )| A. | $\sqrt{5}$-1 | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{\sqrt{5}-1}{2}$ |
分析 根据等腰三角形的性质和三角形内角和计算出图中的所有角,得到AD=BD=BC,易得△ABC∽△BCD,利用相似三角形的性质得$\frac{BC}{CD}$=$\frac{AC}{BC}$,用等线段代换得$\frac{AD}{CD}$=$\frac{AC}{AD}$,则根据黄金分割的定义可判断点D为AC的黄金分割点,所以AD=$\frac{\sqrt{5}-1}{2}$AC=$\sqrt{5}$-1.
解答 解:∵AB=AC=2,
∴∠ABC=∠C=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-36°)=72°,
∵BD平分∠ABC,
∴∠ABD=∠CBD=36°,
∴DA=DB,
而∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BD=BC,
∵∠A=∠CBD,∠C=∠C,
∴△ABC∽△BCD,
∴$\frac{BC}{CD}$=$\frac{AC}{BC}$,即$\frac{AD}{CD}$=$\frac{AC}{AD}$,
∴点D为AC的黄金分割点,
∴AD=$\frac{\sqrt{5}-1}{2}$AC=$\sqrt{5}$-1.
故选A.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.也考查了等腰三角形的性质.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
10.$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$和$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$都是方程y=kx+b的解,则k,b的值分别为( )
| A. | 6,3 | B. | 1,4 | C. | 3,2 | D. | -1,3 |
11.下列说法错误的是( )
| A. | 两个等边三角形一定相似 | B. | 两个等腰三角形一定相似 | ||
| C. | 两个等腰直角三角形一定相似 | D. | 两个全等三角形一定相似 |
8. 如图,将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=( )
如图,将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=( )
 如图,将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=( )
如图,将长为14cm的铁丝AB首尾相接围成半径为2cm的扇形,则S扇形=( )| A. | 12cm2 | B. | 10cm2 | C. | 8cm2 | D. | 6cm2 |
15. 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=22°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=22°,则∠B的度数是( )
 如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=22°,则∠B的度数是( )
如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=22°,则∠B的度数是( )| A. | 67° | B. | 62° | C. | 82° | D. | 72° |
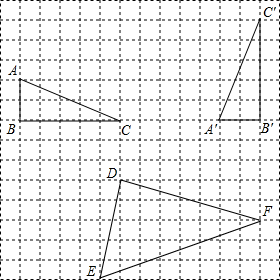 在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:
在如图所示的方格图中,每个小正方形的顶点成为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题: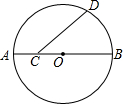 如图,AB为⊙O的直径,C为AB上一点,D为⊙O上一点,且∠DCB=45°,若AC=4,BC=12,求CD的长.
如图,AB为⊙O的直径,C为AB上一点,D为⊙O上一点,且∠DCB=45°,若AC=4,BC=12,求CD的长.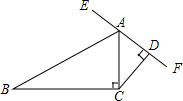 如图,已知AC⊥BC,CD⊥AD,∠B=30°,∠ACD=40°,求图中四边形ABCD的外角的度数.
如图,已知AC⊥BC,CD⊥AD,∠B=30°,∠ACD=40°,求图中四边形ABCD的外角的度数.