题目内容
10．
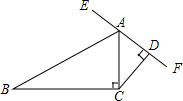如图，已知AC⊥BC，CD⊥AD，∠B=30°，∠ACD=40°，求图中四边形ABCD的外角的度数．
分析 首先根据CD⊥AD，可得∠ADC=90°，再根据直角三角形的性质可得∠BAC=60°，∠DAC=50°，然后再根据平角定义可得答案．
解答 解：∵CD⊥AD，
∴∠ADC=90°，
∴∠FDC=180°-90°=90°，∠DAC+∠ACD=90°，
∵∠ACD=40°，
∴∠DAC=50°，
∵∠B=30°，
∴∠BAC=60°，
∴∠BAD=60°+50°=110°，
∴∠EAB=180°-110°=70°．
点评 此题主要考查了多边形的内角与外角，关键是掌握直角三角形两锐角互余．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
20．
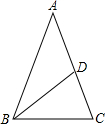如图，在△ABC中，∠A=36°，AB=AC=2，BD平分∠ABC交AC于点D，则AD等于（ ）
如图，在△ABC中，∠A=36°，AB=AC=2，BD平分∠ABC交AC于点D，则AD等于（ ）| A． | $\sqrt{5}$-1 | B． | $\frac{4}{3}$ | C． | 1 | D． | $\frac{\sqrt{5}-1}{2}$ |
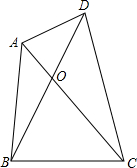如图，S△AOD=3，S△AOB=4，S△COD=6，求S△BOC．
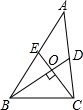如图，已知BD，CE分别是△ABC的两条中线，BD⊥CE于点O，且CE=6，BD=8，则△ABC的面积为32．
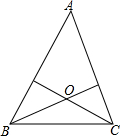已知点O到△ABC的两边AB，AC所在直线的距离相等，且OB=OC，如图，若点O在△ABC的内部，求证：∠ABO=∠ACO．
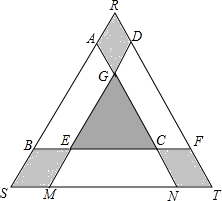某学校矩形数学家“摇篮杯”会徽设计大赛，小明设计的会徽如图所示．正△DEF和正△GMN均由正△ABC平移得到，点A，B，M，N，F，D在正△RST边上，EC=2BE．若阴影部分的面积为$\frac{5\sqrt{3}}{32}$，则正△RST的边长是$\frac{5}{4}$．