题目内容
10.$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$和$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$都是方程y=kx+b的解,则k,b的值分别为( )| A. | 6,3 | B. | 1,4 | C. | 3,2 | D. | -1,3 |
分析 把x与y的两对值代入方程计算即可求出k与b的值.
解答 解:把$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$和$\left\{\begin{array}{l}{x=-1}\\{y=4}\end{array}\right.$分别代入y=kx+b得:$\left\{\begin{array}{l}{k+b=2}\\{-k+b=4}\end{array}\right.$,
解得:k=-1,b=3,
故选D
点评 此题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
20.某校八(1)班积极响应校团委号召,每位同学都向“希望工程”捐献图书,全班40名同学共捐图书320册.特别值得一提的是李扬、王州两位同学在父母的支持下各捐献了50册图书.班长统计了全班捐书情况如表(被粗心的马小虎用墨水污染了一部分)所示:
(1)分别求出该班级捐献7册图书和8册图书的人数.
(2)请算出捐书册数的平均数、中位数和众数.
| 册数 | 4 | 5 | 6 | 7 | 8 | 50 |
| 人数 | 6 | 8 | 15 |  | 2 | |
(2)请算出捐书册数的平均数、中位数和众数.
1.已知$\sqrt{a-2}$+|b+3|=0,那么(a+b)2015的值为( )
| A. | -1 | B. | 1 | C. | 52015 | D. | -52015 |
2.不等式$\left\{\begin{array}{l}{x>2}\\{x<a}\end{array}\right.$无解,则a的取值范围是( )
| A. | a<2 | B. | a>2 | C. | a≤2 | D. | a≥2 |
20.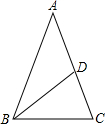 如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
 如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )
如图,在△ABC中,∠A=36°,AB=AC=2,BD平分∠ABC交AC于点D,则AD等于( )| A. | $\sqrt{5}$-1 | B. | $\frac{4}{3}$ | C. | 1 | D. | $\frac{\sqrt{5}-1}{2}$ |
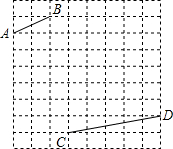 如图的方格纸中,每个小正方形的边长均为1,有线段AB和线段CD,线段的端点均在小正方形的顶点上.
如图的方格纸中,每个小正方形的边长均为1,有线段AB和线段CD,线段的端点均在小正方形的顶点上.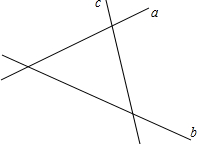 如图,有三条公路a,b,c,为了方便司机休息,路政部门确定修建一个休息站P,使它到三条公路的距离相等.(请用尺规作图,保留作图痕迹,不写作法.)
如图,有三条公路a,b,c,为了方便司机休息,路政部门确定修建一个休息站P,使它到三条公路的距离相等.(请用尺规作图,保留作图痕迹,不写作法.)