题目内容
9．
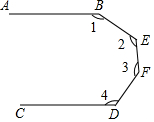如图所示，AB∥CD、BEFD是AB、CD之间的一条折线，则∠1+∠2+∠3+∠4=540°．
分析 连接BD，根据平行线的性质由AB∥CD得到∠ABD+∠CDB=180°，根据四边形的内角和得到∠2+∠3+∠EBD+∠FBD=360°，于是得到结论．
解答 
解：连接BD，如图，
∵AB∥CD，
∴∠ABD+∠CDB=180°，
∵∠2+∠3+∠EBD+∠FBD=360°，
∴∠2+∠3+∠EBD+∠FDB+∠ABD+∠CDB=540°，
即∠1+∠2+∠3+∠4=540°．
故答案为：540°．
点评 本题考查了平行线性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
19．若方程组$\left\{\begin{array}{l}{3x+2y=m+2}\\{2x+3y=m}\end{array}\right.$的解x与y的和为0，则m的值为（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 2 |
20．
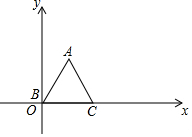已知等边△ABC，顶点B（0，0），C（2，0），规定把△ABC先沿x轴绕着点C顺时针旋转，使点A落在x轴上，称为一次变换，再沿x轴绕着点A顺时针旋转，使点B落在x轴上，称为二次变换，…经过连续2017次变换后，顶点A的坐标是（ ）
已知等边△ABC，顶点B（0，0），C（2，0），规定把△ABC先沿x轴绕着点C顺时针旋转，使点A落在x轴上，称为一次变换，再沿x轴绕着点A顺时针旋转，使点B落在x轴上，称为二次变换，…经过连续2017次变换后，顶点A的坐标是（ ）| A． | （4033，$\sqrt{3}$） | B． | （4033，0） | C． | （4036，$\sqrt{3}$） | D． | （4036，0） |
17．下列分式是最简分式的是（ ）
| A． | $\frac{15bc}{12a}$ | B． | $\frac{{3{{（a-b）}^2}}}{b-a}$ | C． | $\frac{{{a^2}-{b^2}}}{2（a+b）}$ | D． | $\frac{{{a^2}+{b^2}}}{a+b}$ |
1．下列说法正确的是（ ）
| A． | 相等的两个角是对顶角 | |
| B． | 同旁内角相等，两条直线平行 | |
| C． | 两条直线被第三条直线所截，内错角相等 | |
| D． | 同位角相等，两直线平行 |
18．函数y=$\frac{3}{x-1}$中，自变量x的取值范围是（ ）
| A． | x＞1 | B． | x≠3 | C． | x≠1 | D． | x≠0 |