题目内容
19.若方程组$\left\{\begin{array}{l}{3x+2y=m+2}\\{2x+3y=m}\end{array}\right.$的解x与y的和为0,则m的值为( )| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
分析 方程组两方程相加表示出x+y,由x+y=0求出m的值即可.
解答 解:方程组$\left\{\begin{array}{l}{3x+2y=m+2①}\\{2x+3y=m②}\end{array}\right.$,
①+②得:5(x+y)=2m+2,
即x+y=$\frac{2m+2}{5}$,
由题意得:x+y=0,
∴$\frac{2m+2}{5}$=0,
解得:m=-1,
故选C
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
相关题目
10.若m2+m-1=0,则m3+2m2+2017的值为( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
4.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标,则k的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | ±2 |
8. 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )| A. | $\frac{8π}{3}-2\sqrt{3}$ | B. | $\frac{4π}{3}-\sqrt{3}$ | C. | $\frac{8π}{3}-3\sqrt{3}$ | D. | 4$π-\frac{9\sqrt{3}}{4}$ |
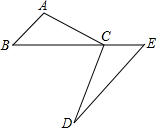 如图,C为BE上一点,点A、D分别在BE两侧,AB∥ED,AB=CE,请你添加一个条件,使△ABC≌△CED,你添加的条件是BC=ED,,并写出证明过程.
如图,C为BE上一点,点A、D分别在BE两侧,AB∥ED,AB=CE,请你添加一个条件,使△ABC≌△CED,你添加的条件是BC=ED,,并写出证明过程.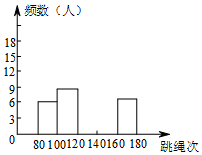 体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
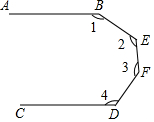 如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=540°.
如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=540°.