题目内容
14.一个多边形的内角和为1620°,则这个多边形的边数是11,这个多边形共可连44条对角线.分析 多边形的内角和可以表示成(n-2)•180°,依此列方程可求多边形的边数;再由多边形的对角线公式求出对角线的条数.
解答 解:设所求正n边形边数为n,
则1620°=(n-2)•180°,
解得n=11;
11边形的对角线共有$\frac{11×(11-3)}{2}$=44条.
故答案为:11;44.
点评 本题考查多边形的内角和定理以及一个n边形共有$\frac{n(n-3)}{2}$条对角线.

练习册系列答案
相关题目
4.若方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标,则k的值为( )
| A. | 2 | B. | 0 | C. | -2 | D. | ±2 |
5.已知菱形ABCD的边长为10,对角线AC=12,则该菱形的面积是( )
| A. | 48 | B. | 48$\sqrt{3}$ | C. | 96 | D. | 96$\sqrt{3}$ |
2.点A(2,y1)、B(3,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
19.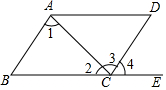 如图所示,下列说法:①∠1与∠3是内错角;②∠B与∠4是同位角;③∠1与∠2是同旁内角;④∠1与∠ACE是内错角,其中正确的有( )
如图所示,下列说法:①∠1与∠3是内错角;②∠B与∠4是同位角;③∠1与∠2是同旁内角;④∠1与∠ACE是内错角,其中正确的有( )
 如图所示,下列说法:①∠1与∠3是内错角;②∠B与∠4是同位角;③∠1与∠2是同旁内角;④∠1与∠ACE是内错角,其中正确的有( )
如图所示,下列说法:①∠1与∠3是内错角;②∠B与∠4是同位角;③∠1与∠2是同旁内角;④∠1与∠ACE是内错角,其中正确的有( )| A. | ①②④ | B. | ①② | C. | ①②③ | D. | ①②③④ |
6.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=3 | D. | $\frac{3}{\sqrt{3}}$=$\sqrt{3}$ |
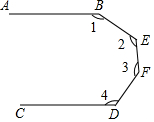 如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=540°.
如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=540°.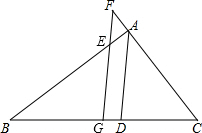 如图,AD是△ABC的角平分线,G是BC中点,FG∥AD,交AB于E,交CA的延长线于F,AC=3.8,AB=7.4,则AF=1.8.
如图,AD是△ABC的角平分线,G是BC中点,FG∥AD,交AB于E,交CA的延长线于F,AC=3.8,AB=7.4,则AF=1.8. 如图,六边形ABCDEF中,AB∥DE,BC∥EF,CD∥AF.现有以下结论:①∠A+∠C+∠E=360°;②∠B+∠C+∠D=360°;③AB=DE.其中正确的结论有( )
如图,六边形ABCDEF中,AB∥DE,BC∥EF,CD∥AF.现有以下结论:①∠A+∠C+∠E=360°;②∠B+∠C+∠D=360°;③AB=DE.其中正确的结论有( )