题目内容
17.下列分式是最简分式的是( )| A. | $\frac{15bc}{12a}$ | B. | $\frac{{3{{(a-b)}^2}}}{b-a}$ | C. | $\frac{{{a^2}-{b^2}}}{2(a+b)}$ | D. | $\frac{{{a^2}+{b^2}}}{a+b}$ |
分析 结合最简分式的定义:一个分式的分子与分母没有公因式时,叫最简分式.求解即可.
解答 解:A、$\frac{15bc}{12a}=\frac{5bc}{4a}$,不是最简分式,本选项错误;
B、$\frac{3(a-b)^{2}}{b-a}=3(b-a)$,不是最简分式,本选项错误;
C、$\frac{{a}^{2}-{b}^{2}}{2(a+b)}=\frac{a-b}{2}$,不是最简分式,本选项错误;
D、$\frac{{a}^{2}+{b}^{2}}{a+b}$,是最简分式,本选项正确;
故选D
点评 本题考查了最简分式,解答本题的关键在于熟练掌握最简分式的定义:一个分式的分子与分母没有公因式时,叫最简分式.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
8. 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )| A. | $\frac{8π}{3}-2\sqrt{3}$ | B. | $\frac{4π}{3}-\sqrt{3}$ | C. | $\frac{8π}{3}-3\sqrt{3}$ | D. | 4$π-\frac{9\sqrt{3}}{4}$ |
5.已知菱形ABCD的边长为10,对角线AC=12,则该菱形的面积是( )
| A. | 48 | B. | 48$\sqrt{3}$ | C. | 96 | D. | 96$\sqrt{3}$ |
12.下列事件是随机事件的是( )
| A. | 购买一张福利彩票,中奖 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 有一名运动员奔跑的速度是80米/秒 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
2.点A(2,y1)、B(3,y2)都在一次函数y=-2x+3的图象上,则y1、y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能确定 |
6.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | 3$\sqrt{2}$-$\sqrt{2}$=3 | D. | $\frac{3}{\sqrt{3}}$=$\sqrt{3}$ |
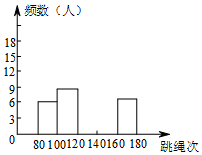 体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
体育老师对九年级(9)班50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示: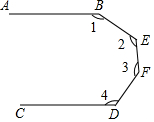 如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=540°.
如图所示,AB∥CD、BEFD是AB、CD之间的一条折线,则∠1+∠2+∠3+∠4=540°.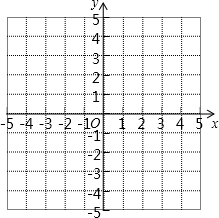 已知等边△ABC两个顶点的坐标为A(-4,0),B(0,0),且点C在第二象限.求:
已知等边△ABC两个顶点的坐标为A(-4,0),B(0,0),且点C在第二象限.求: