题目内容
3.若1≤x≤3时,二次函数y=2x2-3ax+4的最小值为-23,则a=5.分析 分类讨论①当x=1取得最小值.②当x=3取得最小值.③当$\frac{32-9{a}^{2}}{8}$=-23.然后画出草图判定是否符合题意即可.
解答 解:∵1≤x≤3时,二次函数y=2x2-3ax+4的最小值为-23,
∴最小值可能在x=1或3时得到,或最小值=$\frac{4ac-{b}^{2}}{4a}$,
①当x=1取得最小值,2-3a+4=-23,a=$\frac{29}{3}$,此时对称轴x=$\frac{29}{4}$,x=3时有最小值,所以不合题意.
②当x=3取得最小值,18-9a+4=-23,a=5,符合题意.
③当$\frac{32-9{a}^{2}}{8}$=-23,a=±2$\sqrt{6}$,a=2$\sqrt{6}$时,对称轴x=$\frac{3\sqrt{6}}{2}$,x=3时有最小值,不符合题意,
当a=-2$\sqrt{6}$时,对称轴x=-$\frac{3\sqrt{6}}{2}$,x=1时有最小值,不符合题意.
∴a=5,
故答案为5.
点评 本题考查二次函数的最值问题、解题的关键是学会分类讨论,注意这个最小值可以在区间的端点x=1或x=3时取得,属于中考常考题型.

练习册系列答案
相关题目
13.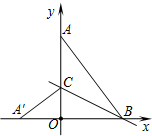 如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )
如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )
 如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )
如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )| A. | y=-$\frac{1}{2}x+\frac{2}{3}$ | B. | y=-x+$\frac{2}{3}$ | C. | y=-$\frac{1}{2}x+\frac{3}{2}$ | D. | y=-2x+$\frac{3}{2}$ |
14.在分别写有数字-1,0,2,3的四张卡片中随机抽取一张,放回后再抽取一张,如果以第一次抽取的数字作为横坐标,第二次抽取的数字作为纵坐标,那么所得点落在第一象限的概率为$\frac{1}{4}$.
12.从正方形纸片上截去3cm宽的一个矩形,余下的面积是40cm2,则原正方形纸片的面积是( )
| A. | 68cm2 | B. | 86cm2 | C. | 64cm2 | D. | 56cm2 |
12.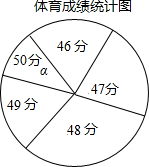 郑州市某中学九年级学生体育中招考试后,为了解本校学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中如扇形统计图中的圆心角α为36°
郑州市某中学九年级学生体育中招考试后,为了解本校学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中如扇形统计图中的圆心角α为36°
九年级学生体育中招成绩统计表
根据上面提供的信息,回答下列问题:
(1)被抽测学生的体育成绩的样本容量为50,m=10;抽取的部分学生体育成绩的中位数为48分;
(2)请计算被抽测学生的中考体育的平均成绩;
(3)已知该校九年级共有500名学生,如果体育成绩达48分以上(含48分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.
 郑州市某中学九年级学生体育中招考试后,为了解本校学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中如扇形统计图中的圆心角α为36°
郑州市某中学九年级学生体育中招考试后,为了解本校学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中如扇形统计图中的圆心角α为36°九年级学生体育中招成绩统计表
| 体育成绩(分) | 人数(人) | 百分比(%) |
| 46 | 8 | 16 |
| 47 | 24 | |
| 48 | 15 | |
| 49 | m | |
| 50 |
(1)被抽测学生的体育成绩的样本容量为50,m=10;抽取的部分学生体育成绩的中位数为48分;
(2)请计算被抽测学生的中考体育的平均成绩;
(3)已知该校九年级共有500名学生,如果体育成绩达48分以上(含48分)为优秀,请估计该校九年级学生体育成绩达到优秀的总人数.