题目内容
13.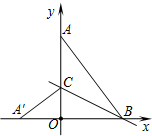 如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )
如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为( )| A. | y=-$\frac{1}{2}x+\frac{2}{3}$ | B. | y=-x+$\frac{2}{3}$ | C. | y=-$\frac{1}{2}x+\frac{3}{2}$ | D. | y=-2x+$\frac{3}{2}$ |
分析 由点A(0,4)、B(3,0),可求得AB的长,然后由折叠的性质,求得OA′的长,且△A′OC∽△AOB,再由相似三角形的性质,求得OC的长,继而利用待定系数法求得直线BC的解析式.
解答 解:∵点A(0,4)、B(3,0),
∴OA=4,OB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=5,
由折叠的性质可得:A′B=AB=5,∠OA′C=∠OAB,
∴OA′=A′B-OB=2,
∵∠A′OC=∠AOB=90°,
∴△A′OC∽△AOB,
∴$\frac{OA′}{OA}=\frac{OC}{OB}$,
即$\frac{2}{4}=\frac{OC}{3}$,
解得:OC=$\frac{3}{2}$,
∴点C的坐标为:(0,$\frac{3}{2}$),
设直线BC的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴直线BC的解析式为:y=-$\frac{1}{2}$x+$\frac{3}{2}$.
故选C.
点评 此题考查了折叠的性质、勾股定理、相似三角形的判定与性质以及待定系数法求一次函数的解析式.注意求得点C的坐标是解此题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
3.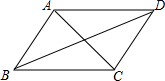 如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )
如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )
 如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )
如图,在平行四边形ABCD中,连接对角线AC、BD,图中的全等三角形的对数( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
8.下列计算正确的是( )
| A. | $\root{3}{27}$=3 | B. | -(-3)2=9 | C. | -(-2)0=1 | D. | |-3|=-3 |
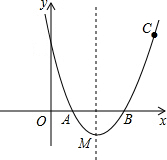 如图,抛物线y=a(x-2)2-1过点C(4,3),交x轴于A,B两点(点A在点B的左侧).
如图,抛物线y=a(x-2)2-1过点C(4,3),交x轴于A,B两点(点A在点B的左侧).