题目内容
7. 已知等边△ABC两个顶点的坐标为A(-4,0),B(0,0),且点C在第二象限.求:
已知等边△ABC两个顶点的坐标为A(-4,0),B(0,0),且点C在第二象限.求:(1)C点的坐标;
(2)△ABC 的面积.
分析 (1)过点C作CD⊥AB于D,根据等边三角形的性质得出BD=2,然后根据勾股定理即可求得CD,从而求得C的坐标;
(2)由三角形面积公式即可求得.
解答 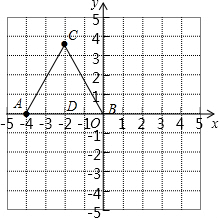 解:(1)过点C作CD⊥AB于D,
解:(1)过点C作CD⊥AB于D,
∵△ABC是等边三角形,A(-4,0),B(0,0),
∴AC=BC=AB=4,
∴BD=$\frac{1}{2}$AB=2,
在Rt△BCD中,∠CDB=90°,
由勾股定理,得:$CD=\sqrt{B{C^2}-B{D^2}}=\sqrt{{4^2}-{2^2}}=\sqrt{12}=2\sqrt{3}$,
∵点C在第二象限
∴C(-2,$2\sqrt{3}$);
(2)S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$×4×$2\sqrt{3}$=$4\sqrt{3}$
点评 此题综合运用了等边三角形的性质和勾股定理,熟练运用三角形的面积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列分式是最简分式的是( )
| A. | $\frac{15bc}{12a}$ | B. | $\frac{{3{{(a-b)}^2}}}{b-a}$ | C. | $\frac{{{a^2}-{b^2}}}{2(a+b)}$ | D. | $\frac{{{a^2}+{b^2}}}{a+b}$ |
18.函数y=$\frac{3}{x-1}$中,自变量x的取值范围是( )
| A. | x>1 | B. | x≠3 | C. | x≠1 | D. | x≠0 |
12.下列关于中点的说法中,正确的是( )
| A. | 若C是线段AB上的一点,且AC+CB=AB,则点C是AB的中点 | |
| B. | 若平面上有线段AB和一点C,且AC=CB,则点C是线段AB的中点 | |
| C. | 若C是线段AB上的一点,且AC=2CB,则点C是AB的中点 | |
| D. | 若延长线段AC到B,且AC=CB,则点C是线段AB的中点 |
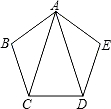 如图,在正五边形ABCDE中,AC、AD为对角线,则∠CAD的大小为36°.
如图,在正五边形ABCDE中,AC、AD为对角线,则∠CAD的大小为36°.