题目内容
8. 如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )
如图,等边△ABC内接于⊙O,已知⊙O的半径为2,则图中的阴影部分面积为( )| A. | $\frac{8π}{3}-2\sqrt{3}$ | B. | $\frac{4π}{3}-\sqrt{3}$ | C. | $\frac{8π}{3}-3\sqrt{3}$ | D. | 4$π-\frac{9\sqrt{3}}{4}$ |
分析 连接OB、OC,连接AO并延长交BC于H,根据等边三角形的性质求出△OBC的面积,根据扇形面积公式、结合图形计算即可.
解答 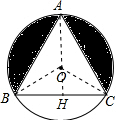 解:连接OB、OC,连接AO并延长交BC于H,
解:连接OB、OC,连接AO并延长交BC于H,
则AH⊥BC,
∵△ABC是等边三角形,
∴BH=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$,OH=1,
∴△OBC的面积=$\frac{1}{2}$×BC×OH=$\sqrt{3}$,
则△OBA的面积=△OAC的面积=△OBC的面积=$\sqrt{3}$,
由圆周角定理得,∠BOC=120°,
∴图中的阴影部分面积=$\frac{240π×{2}^{2}}{360}$-2$\sqrt{3}$=$\frac{8}{3}$π-2$\sqrt{3}$,
故选:A.
点评 本题考查的是三角形的外接圆与外心、扇形面积的计算,掌握等边三角形的性质、扇形面积公式是解题的关键.

练习册系列答案
相关题目
18.$\sqrt{9}+\sqrt{16}$的值是( )
| A. | 7 | B. | -1 | C. | 1 | D. | -7 |
19.若方程组$\left\{\begin{array}{l}{3x+2y=m+2}\\{2x+3y=m}\end{array}\right.$的解x与y的和为0,则m的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
13.已知直线y=x+$\frac{3}{2}$与直线y=kx-1相交于点P,若点P的纵坐标为$\frac{1}{2}$,则关于x的不等式x+$\frac{3}{2}$>kx-1的解集为( )
| A. | x>-1 | B. | x≥-1 | C. | x<-1 | D. | x≤-1 |
20.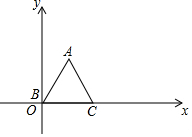 已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
 已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )
已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2017次变换后,顶点A的坐标是( )| A. | (4033,$\sqrt{3}$) | B. | (4033,0) | C. | (4036,$\sqrt{3}$) | D. | (4036,0) |
17.下列分式是最简分式的是( )
| A. | $\frac{15bc}{12a}$ | B. | $\frac{{3{{(a-b)}^2}}}{b-a}$ | C. | $\frac{{{a^2}-{b^2}}}{2(a+b)}$ | D. | $\frac{{{a^2}+{b^2}}}{a+b}$ |
18.函数y=$\frac{3}{x-1}$中,自变量x的取值范围是( )
| A. | x>1 | B. | x≠3 | C. | x≠1 | D. | x≠0 |
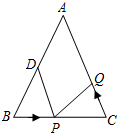 如图,在△ABC中,AB=AC=10厘米,BC=8厘米,D为AB的中点,点P在线段BC上以3厘米/秒的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
如图,在△ABC中,AB=AC=10厘米,BC=8厘米,D为AB的中点,点P在线段BC上以3厘米/秒的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.