题目内容
20.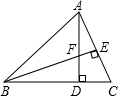 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.(1)求证:△ACD∽△BFD;
(2)当$\frac{AD}{BD}$=1,AC=3时,求BF的长.
分析 (1)只要证明∠DBF=∠DAC,即可判断.
(2)利用相似三角形的性质即可解决问题.
解答 (1)证明:如图,∵AD⊥BC,BE⊥AC
∴∠BDF=∠ADC=∠BEC=90°
∴∠C+∠DBF=90°,∠C+∠DAC=90°
∴∠DBF=∠DAC
∴△ACD∽△BFD
(2)解:如图,∵$\frac{AD}{BD}$=1,△ACD∽△BFD,AC=3,
∴$\frac{AC}{BF}$=$\frac{AD}{BD}$=1,
∴BF=AC=3.
点评 本题考查相似三角形的性质和判定,同角的余角相等,直角三角形两锐角互余等知识,解题的关键是正确寻找相似三角形,利用新三角形的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
10. 如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
 如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )
如图所示,点A(-1,m),B(3,n)在一次函数y=kx+b的图象上,则( )| A. | m=n | B. | m>n | ||
| C. | m<n | D. | m、n的大小关系不确定 |
5.若分式方程$\frac{x+2}{x+3}=\frac{m}{x+3}$无解,则m的值为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 3 |
9.在数1、2、3和4中,是方程x2+x-12=0的根的为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 补全解题过程.
补全解题过程.