题目内容
8．
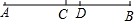补全解题过程．已知：如图，点C是线段AB的中点，AD=6，BD=4，求CD的长．
解：∵AD=6，BD=4，
∴AB=AD+BD=10．
∵点C是线段AB的中点，
∴AC=CB=$\frac{1}{2}$AB=5．
∴CD=AD-AC=1．
分析 根据线段的和差，可得AB的长，根据线段中点的性质，可得AC的长，再根据线段的和差，可得答案．
解答 解：：∵AD=6，BD=4，
∴AB=AD+BD=10．
∵点C是线段AB的中点，
∴AC=CB=$\frac{1}{2}$AB=5．
∴CD=AD-AC=1．
故答案为：BD，10；$\frac{1}{2}$AB，5；AC，1．
点评 本题考查了两点间的距离，利用线段中点的性质得出AC的长是解题关键
练习册系列答案
相关题目
18．将三角形三个顶点的横坐标都减2，纵坐标不变，则所得三角形与原三角形的关系是（ ）
| A． | 将原三角形向左平移两个单位 | B． | 将原三角形向右平移两个单位 | ||
| C． | 关于x轴对称 | D． | 关于y轴对称 |
19．
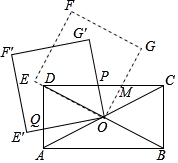如图，矩形ABCD的对角线交于点O，正方形OEFG的一条边OE在直线OD上，OG与CD交于点M，正方形OEFG绕点O逆时针旋转，OG′，OE′分别与CD，AD交于点P，Q．已知矩形长与宽的比值为2，则在旋转过程中PM：DQ=（ ）
如图，矩形ABCD的对角线交于点O，正方形OEFG的一条边OE在直线OD上，OG与CD交于点M，正方形OEFG绕点O逆时针旋转，OG′，OE′分别与CD，AD交于点P，Q．已知矩形长与宽的比值为2，则在旋转过程中PM：DQ=（ ）| A． | 1：3 | B． | 2：3 | C． | 1：2 | D． | 3：4 |
16．
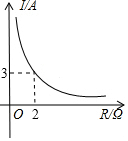已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．则用电阻R表示电流I的函数表达式为（ ）
已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示．则用电阻R表示电流I的函数表达式为（ ）| A． | $I=\frac{3}{R}$ | B． | $I=-\frac{6}{R}$ | C． | $I=-\frac{3}{R}$ | D． | $I=\frac{6}{R}$ |
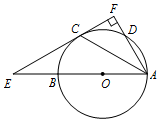如图，AB是⊙O的直径，C，D是⊙O上两点，且$\widehat{BC}$=$\widehat{CD}$，过点C的直线CF⊥AD于点F，交AB的延长线于点E，连接AC．
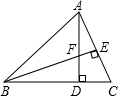如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．