题目内容
1．
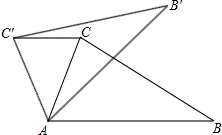如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB′C′的位置，使得CC′∥AB，则∠BAB′=（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 50° |
分析 首先证明∠ACC′=∠AC′C；然后运用三角形的内角和定理求出∠CAC′=30°即可解决问题．
解答 解：由题意得：
AC=AC′，
∴∠ACC′=∠AC′C；
∵CC′∥AB，且∠BAC=75°，
∴∠ACC′=∠AC′C=∠BAC=75°，
∴∠CAC′=180°-2×75°=30°；
由题意知：∠BAB′=∠CAC′=30°，
故选A
点评 该命题以三角形为载体，以旋转变换为方法，综合考查了全等三角形的性质及其应用问题；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
阅读快车系列答案
相关题目
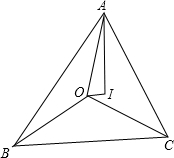在△ABC中，AB＞AC，O、I分别是△ABC的外心和内心，且满足AB-AC=2OI，求证：