题目内容
10.(1)请观察下列算式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,$\frac{1}{4×5}$=$\frac{1}{4}$-$\frac{1}{5}$,…,则第10个算式为$\frac{1}{10×11}$=$\frac{1}{10}$-$\frac{1}{11}$,
第n个算式为$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)运用以上规律计算:$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+…+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$.
分析 (1)直接将分数拆项变形即可;
(2)原式拆项变形后,抵消合并即可得到结果.
解答 解:(1)第10个算式为$\frac{1}{10×11}$=$\frac{1}{10}$-$\frac{1}{11}$,
第n个算式为 $\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)$\frac{1}{2}$+$\frac{1}{6}$+$\frac{1}{12}$+…+$\frac{1}{90}$+$\frac{1}{110}$+$\frac{1}{132}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{11}$-$\frac{1}{12}$
=1-$\frac{1}{12}$
=$\frac{11}{12}$.
故答案为:$\frac{1}{10×11}$,$\frac{1}{10}$-$\frac{1}{11}$;$\frac{1}{n(n+1)}$,$\frac{1}{n}$-$\frac{1}{n+1}$.
点评 此题考查了有理数的加法,熟练掌握拆项的方法是解本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
1.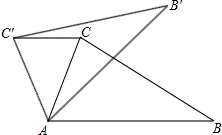 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
 如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )
如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
19.不等式6x+5>3x+8的解集为( )
| A. | x>2 | B. | x>1 | C. | x<1 | D. | x<2 |
 如图,AB是⊙O的直径,AC、BD是⊙O的切线,切点分别为A、B,EF分别交AC、BD于点E、F,且EO平分∠AEF.
如图,AB是⊙O的直径,AC、BD是⊙O的切线,切点分别为A、B,EF分别交AC、BD于点E、F,且EO平分∠AEF.