题目内容
8. 已知A(2,-2),B(-1,4)是一次函数y2=-2x+2的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.
已知A(2,-2),B(-1,4)是一次函数y2=-2x+2的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.(1)反比例函数关系式为y=-$\frac{4}{x}$;
(2)直接写出方程kx+b=$\frac{m}{x}$的解;
(3)观察图象,写出当x为何值时,y1<y2;
(4)求△AOB的面积.
分析 (1)把B点坐标代入反比例函数解析式可求得反比例函数解析式;
(2)根据函数和方程的关系直接求得;
(3)根据图象和交点坐标即可求得;
(4)根据一次函数解析式可求得C点的坐标,则可求得OC的长度,且根据△AOB的面积=△BOC的面积+△AOC的面积,可求得△AOB的面积.
解答 解:(1)∵B点在反比例函数的图象上,
∴m=-1×4=-4,
∴反比例函数解析式为y=-$\frac{4}{x}$,
故答案为y=-$\frac{4}{x}$;
(2)∵A(2,-2),B(-1,4)是一次函数y2=-2x+2的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点,
∴方程kx+b=$\frac{m}{x}$的解是2和-1;
(3)观察图象,当-1<x<0或x>2时,y1<y2;
(4)由一次函数y2=-2x+2可知C(0,2),
∴△AOB的面积=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×2=3.
点评 本题主要考查待定系数法求函数解析式,函数和方程的关系函数和不等式的关系以及三角形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.-(-2)的相反数是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -$\frac{1}{2}$ |
16.若x,y都是有理数,且|4-3x+y|与(3-4x-y)2互为相反数,则x,y的值分别为( )
| A. | x=-1,y=2 | B. | x=1,y=-1 | C. | x=0,y=-$\frac{3}{5}$ | D. | x=3,y=1 |
14.下列计算中,结果正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a6 | C. | (2a)(3a)=6a | D. | a6÷a2=a3 |
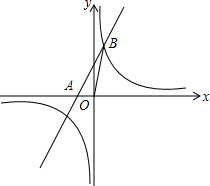 如图,直线y=2x+3与反比例函数y=$\frac{k}{x}$的图象相交于点B(a,5),且与x轴相交于点A.
如图,直线y=2x+3与反比例函数y=$\frac{k}{x}$的图象相交于点B(a,5),且与x轴相交于点A.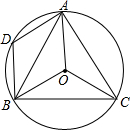 如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.
如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.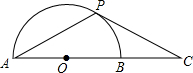 如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA
如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA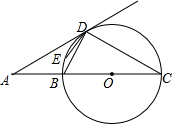 如图,BC是⊙O的直径,延长CB到点A使AB=$\frac{1}{2}$CB,过点A作射线AD,使AD与⊙O相切于点D,连接BD,CD.若点E是劣弧$\widehat{BD}$上一点,则∠BED的度数为150°.
如图,BC是⊙O的直径,延长CB到点A使AB=$\frac{1}{2}$CB,过点A作射线AD,使AD与⊙O相切于点D,连接BD,CD.若点E是劣弧$\widehat{BD}$上一点,则∠BED的度数为150°.