题目内容
3．
如图，AB∥CD，∠A=40°，∠E=25°，则∠C等于65°．
分析 根据外角的性质，求出∠EFB的度数，根据AB∥CD，求出∠C的度数．
解答 解：∠EFB=∠E+∠A=65°，
∵AB∥CD，
∴∠C=∠EFB=65°．
故答案为：65°．
点评 本题考查的是平行线的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．在解答时，要结合图形，正确运用性质．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
14．
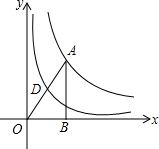如图，Rt△OAB的直角边OB在x轴上，反比例函数y=$\frac{4}{x}$在第一象限的图象经过其顶点A，点D为斜边OA的中点，另一个反比例函数y1=$\frac{k}{x}$在第一象限的图象经过点D，则k的值为（ ）
如图，Rt△OAB的直角边OB在x轴上，反比例函数y=$\frac{4}{x}$在第一象限的图象经过其顶点A，点D为斜边OA的中点，另一个反比例函数y1=$\frac{k}{x}$在第一象限的图象经过点D，则k的值为（ ）| A． | 1 | B． | 2 | C． | $\frac{1}{2}$ | D． | 无法确定 |
18．有关媒体报道2014年“双十一”，天猫电商平台整体交易额突破570亿，570亿用科学记数法表示为（ ）
| A． | 5.7×1011 | B． | 5.7×1010 | C． | 0.57×1011 | D． | 0.57×1012 |
如图，为测量某建筑物BC及上面旗杆AB的高度，小明在距建筑物BC底部12m的点F处，测得视线点E与旗杆AB的顶端A的仰角为52°，测得视线点E与旗杆AB的底端B是仰角为45°，已知小明的身高EF为1.6m．
15．甲乙两人在相同的时间内各加工168个零件和144个零件，已知甲每小时比乙多加工8个零件，求乙每小时加工多少个零件．设乙每小时加工x个零件，可列方程为（ ）
| A． | $\frac{168}{x}$=$\frac{144}{x-8}$ | B． | $\frac{168}{x}$=$\frac{144}{x+8}$ | C． | $\frac{168}{x-8}$=$\frac{144}{x}$ | D． | $\frac{168}{x+8}$=$\frac{144}{x}$ |
如图，已知点A，B，C，D在⊙O上，AC⊥BD，垂足为P，OE⊥AB，垂足为E，点F为CD中点，连接OF，PE，PF，试判断四边形OFPE的形状，并说明理由．