题目内容
16．如果扇形的半径为5，弧长为6π，那么不重合，无缝隙地折叠成圆锥的体积为12π．分析 利用圆锥的底面圆周长等于扇形的弧长可求出半径，再利用轴截面及勾股定理即可求出圆锥的高，进而计算出体积．
解答 解：设此圆锥的底面半径为r，由题意得2πr=6π，
∴r=3．
由勾股定理得圆锥的高为：$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴V圆锥=$\frac{1}{3}$×π×32×4=12π．
故答案为12π．
点评 此题考查了用扇形纸片围成一个圆锥并计算其体积，利用已知条件画出图形及理解圆锥的体积公式是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
7．下列图形既可看成轴对称图形又可看成中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
4．甲、乙两班参加市统考，两班的平均分和方差分别为$\overline{{X}_{甲}}$=86分，$\overline{{X}_{乙}}$=86分，S甲2=263，S乙2=236，那么成绩较为整齐的是（ ）
| A． | 甲班 | B． | 乙班 | C． | 两班一样整齐 | D． | 无法确定 |
1．
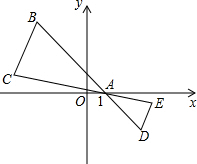如图，在△ABC中，B，C两个顶点在x轴的上方，点A的坐标是（1，0），以点A为位似图形，并把△ABC的边长缩小为原来的$\frac{1}{2}$倍，记所得的位似图形为△ADE．设点C的对应点E的横坐标为a，则点C的横坐标为（ ）
如图，在△ABC中，B，C两个顶点在x轴的上方，点A的坐标是（1，0），以点A为位似图形，并把△ABC的边长缩小为原来的$\frac{1}{2}$倍，记所得的位似图形为△ADE．设点C的对应点E的横坐标为a，则点C的横坐标为（ ）| A． | $\frac{1}{2}$（a-1） | B． | $\frac{1}{2}$（a+1） | C． | 3-2a | D． | 2（a-1） |
如图，为测量某建筑物BC及上面旗杆AB的高度，小明在距建筑物BC底部12m的点F处，测得视线点E与旗杆AB的顶端A的仰角为52°，测得视线点E与旗杆AB的底端B是仰角为45°，已知小明的身高EF为1.6m．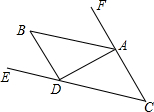
如图，已知AB∥CD，AB是∠FAD的平分线，∠C=45°．