题目内容
 如图,在矩形ABCD中,AB=6cm,BC=4cm,M是CD的中点,求点B到直线AM的距离.
如图,在矩形ABCD中,AB=6cm,BC=4cm,M是CD的中点,求点B到直线AM的距离.考点:矩形的性质,勾股定理,相似三角形的判定与性质
专题:
分析:根据线段中点的定义求出DM,利用勾股定理列式求出AM,过点B作BN⊥AM于N,求出△ABN和△MAD相似,利用相似三角形对应边成比例列式计算即可得解.
解答: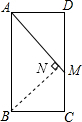 解:∵M是CD的中点,
解:∵M是CD的中点,
∴DM=
CD=
AB=
×6=3cm,
由勾股定理得,AM=
=
=5cm,
过点B作BN⊥AM于N,
∵∠ABN+∠BAN=90°,∠BAN+∠DAM=90°,
∴∠ABN=∠DAM,
又∵∠D=∠ANB=90°,
∴△ABN∽△MAD,
∴
=
,
即
=
,
解得BN=
,
即点B到直线AM的距离为
cm.
 解:∵M是CD的中点,
解:∵M是CD的中点,∴DM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由勾股定理得,AM=
| AD2+DM2 |
| 42+32 |
过点B作BN⊥AM于N,
∵∠ABN+∠BAN=90°,∠BAN+∠DAM=90°,
∴∠ABN=∠DAM,
又∵∠D=∠ANB=90°,
∴△ABN∽△MAD,
∴
| BN |
| AD |
| AB |
| AM |
即
| BN |
| 4 |
| 6 |
| 5 |
解得BN=
| 24 |
| 5 |
即点B到直线AM的距离为
| 24 |
| 5 |
点评:本题考查了矩形的性质,勾股定理,相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键.

练习册系列答案
相关题目
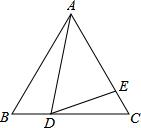 已知边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AD=
已知边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AD= 如图,已知∠A=∠B=90°,AB=7、AD=2、BC=3,P在AB上,且△PAD∽△PBC,求AP的长.
如图,已知∠A=∠B=90°,AB=7、AD=2、BC=3,P在AB上,且△PAD∽△PBC,求AP的长.