Question

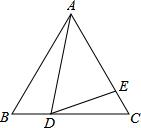已知边长为9的正三角形ABC中，BD=3，∠ADE=60°，则AD=

 

．

Answer 1

考点：相似三角形的判定与性质,等边三角形的性质

专题：

分析：过A作AF⊥BC于F，根据等边三角形的性质求出AB=BC=AC=9，∠B=∠C=60°，求出BF=CF=4.5，由勾股定理求出AF，求出DF=1.5，在Rt△AFD中，由勾股定理求出AD即可．

解答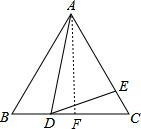：解：过A作AF⊥BC于F，
∵△BAC是等边三角形，
∴AB=BC=AC=9，∠B=∠C=60°，
∴BF=CF=4.5，
由勾股定理得：AF=

AB2-BF2

=

92-4．52

=

9

2

3

，
∵BD=3，BF=4.5，
∴DF=1.5，
在Rt△AFD中，由勾股定理得：AD=

AF2-DF2

=

( 9 2 3 )2-1．52

=

3 26

2

，
故答案为：

3 26

2

．

点评：本题考查了等边三角形的性质，等腰三角形的性质，勾股定理的应用，解此题的关键是求出AF和DF的长．