题目内容
3.观察下列计算$\frac{1}{1×2}=1-\frac{1}{2}$,$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$,$\frac{1}{4×5}=\frac{1}{4}-\frac{1}{5}$,…
(1)第5个式子是$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$;第n个式是$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
(2)从计算结果中找规律,利用规律计算$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+\frac{1}{4×5}+$…+$\frac{1}{2009×2010}$.
(3)计算$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+$…+$\frac{1}{(2n-1)×(2n+1)}$.
分析 (1)观察一系列等式得到一般性规律,写出第5个式子与第n个式子即可;
(2)原式利用得出的规律化简,计算即可得到结果;
(3)原式变形后,利用得出的规律化简,计算即可得到结果.
解答 解:(1)第5个式子是$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$;$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
故答案为:$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$;$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)原式=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{2009}$-$\frac{1}{2010}$)
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{2009}$-$\frac{1}{2010}$
=1-$\frac{1}{2010}$
=$\frac{2009}{2010}$;
(3)原式=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案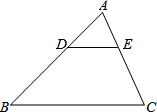 如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则$\frac{DE}{BC}$=( )
如图,在△ABC中,DE∥BC,$\frac{AD}{BD}$=$\frac{1}{2}$,则$\frac{DE}{BC}$=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
| A. | (+3)-|-3| | B. | |+3|+|-3| | C. | (-3)-3 | D. | $\frac{2}{3}+$(-$\frac{3}{2}$) |
| A. | 10 | B. | 7 | C. | -10 | D. | -7 |
| A. | 4xy-3xy=1 | B. | 2b2c+3b2c=6b2c | C. | 2a2+3a2=5a2 | D. | 2m2n-2mn2=0 |




 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.