题目内容
13. 如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.
如图,在△ABA1中,∠B=20°,AB=A1B,在A1B上取一点B1,延长AA1到A2,使得A1A2=A1B1,连接A2B1,在A2B1上取一点B2,延长A1A2到A3,使得A2A3=A2B2;…,按此作法进行下去,∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.
分析 先根据等腰三角形的性质求出∠BA1A的度数,再根据三角形外角的性质及等腰三角形的性质分别求出∠B1A2A1,∠B2A3A2及∠B3A4A3的度数,找出规律即可得出∠A2015A2016B2015的度数.
解答 解:∵在△ABA1中,∠B=20°,AB=A1B,
∴∠BA1A=$\frac{180°-∠B}{2}$=80°,
∵A1A2=A1B1,∠BA1A是△A1A2B1的外角,
∴∠B1A2A1=$\frac{∠B{A}_{1}A}{2}$=40°;
同理可得,
∠B2A3A2=20°,∠B3A4A3=10°,
∴∠An-1AnBn-1=$\frac{80°}{{2}^{n-1}}$,
∴∠A2015A2016B2015的度数为$\frac{80°}{{2}^{2015}}$.
故答案为:$\frac{80°}{{2}^{2015}}$.
点评 本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠B1C2A1,∠B2A3A2及∠B3A4A3的度数,找出规律是解答此题的关键.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 如图,AC=4,BC=6,∠B=36°,∠D=117°,△ABC∽△DAC.求:
如图,AC=4,BC=6,∠B=36°,∠D=117°,△ABC∽△DAC.求: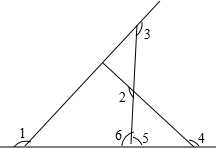 如图,求∠1+∠2+∠3+∠4的度数.
如图,求∠1+∠2+∠3+∠4的度数.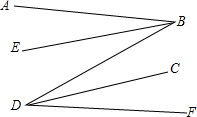 如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?
如图,AB∥DF,BE,DC分别是∠ABD,∠FDB的平分线,BE∥DC吗?为什么?