题目内容
8.已知直线y=2x+4与x轴、y轴的交点分别为A、B,y轴上点C的坐标为(0,2),找一点P,使得以P、A、B、C为顶点的四边形是平行四边形,则点P的坐标为(-2,-2)或(-2,2)或(2,6).分析 由一次函数的解析式求出点A和B的坐标,得出OA、OB、BC,分别求出以AC、AB、BC为对角线时点P的坐标即可.
解答 解:直线y=2x+4,当y=0时,x=-2,当x=0时,y=4,
∴A(-2,0),B(0,4),
∴OB=4,OA=2,
∵点C的坐标为(0,2),
∴OC=2,
∴BC=2,
当AC为对角线时,点P的坐标为(-2,-2);
当AB为对角线时,点P的坐标为(-2,2);
当BC为对角线时,点P的坐标为(2,6).
综上所述:以P、A、B、C为顶点的四边形是平行四边形时,则点P的坐标为(-2,-2)或(-2,2)或(2,6).
点评 本题考查了平行四边形的判定、一次函数的运用;熟练掌握平行四边形的判定方法,分情况讨论求出点P的坐标是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 3$\sqrt{2}$ | D. | $\sqrt{6}$ |
 如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.
如图,AP∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的延长线交AP于D.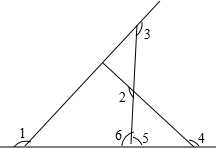 如图,求∠1+∠2+∠3+∠4的度数.
如图,求∠1+∠2+∠3+∠4的度数.