题目内容
14．
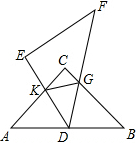如图．将两块完全一样的透明等腰直角角形板ABC、DEF按如图所示的方式放置，使点D落在线段AB的中点处，直角边DE与直角边AC相交于点K，斜边DF与直角边相交于点G，连接KG．（1）求证：△ADK∽△BGD．
（2）求证：△ADK∽△DGK．
（3）若AC=BC=8，KG=x，△DGK的面积为y，请求出y与x的函数表达式．（不需要写出x的取值范围）
分析 （1）由三角形ABC为等腰直角三角形得到一对角相等，再利用等式的性质得到一对角相等，利用两角相等的三角形相似即可得证；
（2）由（1）的结论，利用相似三角形对应成比例，根据D为AB中点，代换后再根据夹角相等，利用两边对应成比例且夹角相等的三角形相似即可得证；
（3）如图所示：过D作AC，KG的垂线，垂足分别为M，N，由KD为角平分线，利用角平分线定理得到DM=DN，利用AAS得到三角形MDK与三角形NDK全等，利用全等三角形对应边相等得到DM=DN，求出DM的长即为DN的长，三角形DKG面积以KG为底边，DN为高，利用三角形面积公式列出y与x的函数表达式即可．
解答 （1）证明：∵∠KAD=∠KDG=∠B=45°，∠KAD+∠BDG=135°，∠DGB+∠BDG=135°，
∴∠KAD=∠DGB，
∴△ADK∽△BGD；
（2）证明：∵△ADK∽△BGD，
∴$\frac{AK}{BD}$=$\frac{KD}{DG}$，
∵D为AB的中点，
∴BD=AD，
∴$\frac{AK}{AD}$=$\frac{KD}{DG}$，即$\frac{AK}{KD}$=$\frac{AD}{DG}$，
∵∠KAD=∠KDG=45°，
∴△AKD∽△DKG；
（3）解：如图所示：过D作AC，KG的垂线，垂足分别为M，N，
∵KD平分∠AKG，
∴∠MKD=∠NKD，
在△MKD和△NKD中，
$\left\{\begin{array}{l}{∠DMK=∠DNK}\\{∠MKD=∠NKD}\\{KD=KD}\end{array}\right.$，
∴△MKD≌△NKD（AAS），
∴DM=DN，
∵D为AB的中点，∠KAD=45°，
∴AM=DM=$\frac{1}{2}$AC=4，
∴DN=4，
∴S△DKG=$\frac{1}{2}$×DN×KG=$\frac{1}{2}$×4×x=2x，即y=2x（8$\sqrt{2}$-8≤x≤8$\sqrt{3}$-8）．
点评 此题属于相似形综合题，涉及的知识有：相似三角形的判定与性质，全等三角形的判定与性质，等腰直角三角形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．
