题目内容
5.对任意的有理数a,b,c,d,我们规定一种运算:$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc.若$|\begin{array}{l}{-5}&{3{x}^{2}+5}\\{2}&{{x}^{2}-3}\end{array}|$=5,则11x2-5的值为-5.分析 已知等式利用已知的新定义变形,整理求出11x2的值,代入原式计算即可得到结果.
解答 解:根据题中的新定义得:-5(x2-3)-2(3x2+5)=5,
整理得:11x2=0,
则原式=0-5=-5.
故答案为:-5
点评 此题考查了整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17.掷两枚骰子,得到2点的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{36}$ |
 在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求证:AB2=BD•BC.
在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求证:AB2=BD•BC.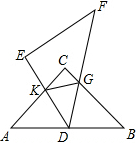 如图.将两块完全一样的透明等腰直角角形板ABC、DEF按如图所示的方式放置,使点D落在线段AB的中点处,直角边DE与直角边AC相交于点K,斜边DF与直角边相交于点G,连接KG.
如图.将两块完全一样的透明等腰直角角形板ABC、DEF按如图所示的方式放置,使点D落在线段AB的中点处,直角边DE与直角边AC相交于点K,斜边DF与直角边相交于点G,连接KG.