题目内容
2.已知直线y=(1-3k)x+2k-1,求:(1)k为何值时,直线过原点;
(2)k为何值时,直线与y轴的交点坐标为(0,-2);
(3)k为何值时,直线与x轴交于点($\frac{3}{4}$,0);
(4)k为何值时,y的值随着x的增大而增大;
(5)k为何值时,该直线与直线y=-3x-5平行.
分析 (1)把原点的坐标(0,0)代入y=(1-3k)x+2k-1,得到关于k的方程,解方程即可;
(2)将点(0,-2)代入y=(1-3k)x+2k-1,得到关于k的方程,解方程即可;
(3)将点($\frac{3}{4}$,0)代入y=(1-3k)x+2k-1,得到关于k的方程,解方程即可;
(4)根据一次函数的性质得出1-3k>0,解不等式即可;
(5)根据两条直线平行的条件得出1-3k=-3,2k-1≠-5,求出即可.
解答 解:(1)∵直线y=(1-3k)x+2k-1经过原点,
∴2k-1=0,
解得:k=$\frac{1}{2}$;
(2)∵直线y=(1-3k)x+2k-1与y轴的交点坐标为(0,-2),
∴2k-1=-2,
解得:k=-$\frac{1}{2}$;
(3)∵直线y=(1-3k)x+2k-1与x轴交于点($\frac{3}{4}$,0);
∴$\frac{3}{4}$(1-3k)+2k-1=0,
解得:k=-1;
(4)∵直线y=(1-3k)x+2k-1中y的值随着x的增大而增大,
∴1-3k>0,
∴k<$\frac{1}{3}$;
(4)∵直线y=(1-3k)x+2k-1与直线y=-3x+5平行,
∴1-3k=-3,2k-1≠-5,
∴k=$\frac{4}{3}$.
点评 本题考查了一次函数的性质,一次函数图象上点的坐标特征,两条直线平行的条件,是基础知识,需熟练掌握.

练习册系列答案
相关题目
17.掷两枚骰子,得到2点的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{36}$ |
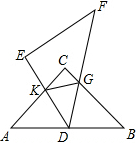 如图.将两块完全一样的透明等腰直角角形板ABC、DEF按如图所示的方式放置,使点D落在线段AB的中点处,直角边DE与直角边AC相交于点K,斜边DF与直角边相交于点G,连接KG.
如图.将两块完全一样的透明等腰直角角形板ABC、DEF按如图所示的方式放置,使点D落在线段AB的中点处,直角边DE与直角边AC相交于点K,斜边DF与直角边相交于点G,连接KG.