题目内容
14.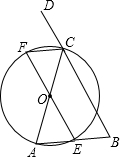 如图,在△ABC中,AC=BC,以AC为直径作⊙O交AB于E,作∠BCA的外角平分线CF交⊙O于F,连接EF.那么EF与BC相等吗?为什么?
如图,在△ABC中,AC=BC,以AC为直径作⊙O交AB于E,作∠BCA的外角平分线CF交⊙O于F,连接EF.那么EF与BC相等吗?为什么?
分析 根据等腰三角形三线合一的性质得出∠A=∠B,再由同弧所对的圆周角相等得∠A=∠F,由OC=OF得出∠F=∠OCF,则∠A=∠OCF,由平行线的判定定理得出CF∥AB,同理得出EF∥BC,四边形BCFE是平行四边形,得出EF=BC.
解答 解:EF=BC,
理由是:∵AC=BC,
∴∠A=∠B,
∵∠A=∠F,
∴∠B=∠F,
∵OC=OF,
∴∠F=∠OCF,
∴∠A=∠OCF,
∴CF∥AB,
同理得EF∥BC,
∴四边形BCFE是平行四边形,
∴EF=BC
点评 本题考查了圆周角定理以及平行线的判定和方法,掌握平行线的判定和方法是解题的关键.

练习册系列答案
相关题目
5.若(2,5),(4,5)是抛物线y=ax2+bx+c上的两个点,则它的对称轴是( )
| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=4 |
3. 如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CD交AO于点E,DE=4,CE=5,则tan∠B的值为( )
如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CD交AO于点E,DE=4,CE=5,则tan∠B的值为( )
 如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CD交AO于点E,DE=4,CE=5,则tan∠B的值为( )
如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CD交AO于点E,DE=4,CE=5,则tan∠B的值为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
4.某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?
(1)请你在下表的空格里填写一个适当的式子:
| 第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
| a | a+2 | a+4 | … |
(3)求当a=20时,第10排的座位数是多少?
 已知Rt△ABC中∠C=90°,AC=3,BC=4,以三角形一条边为边画等腰三角形,使它的第三个顶点在△ABC的其他边上,则这样的点有( )个.
已知Rt△ABC中∠C=90°,AC=3,BC=4,以三角形一条边为边画等腰三角形,使它的第三个顶点在△ABC的其他边上,则这样的点有( )个.