题目内容
19．求值：$\frac{（201{6}^{2}-2022）（201{6}^{2}+4029）×2017}{2013×2015×2018×2019}$=2017．分析 原式分子中两个括号中变形后，利用十字相乘法计算得到结果，代入原式约分即可得到结果．
解答 解：∵20162-2022=（2022-6）2-2022=20222-12×2022+36-2022=20222-13×2022+36=（2022-4）×（2022-9）=2018×2013，
20162+4029=（2022-6）2+2×2022-15=20222-10×2022+21=（2022-3）×（2022-7）=2019×2015，
∴原式=$\frac{2018×2013×2019×2015×2017}{2013×2015×2018×2019}$=2017．
故答案为：2017
点评 此题考查了平方差公式，将括号中两式进行适当的变形是解本题的关键．
练习册系列答案
相关题目
用四个全等的直角三角形拼成了一个如图所示的图形，其中a表示较短直角边，b表示较长的直角边，c表示斜边，你能用这个图形证明勾股定理吗？
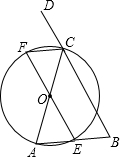如图，在△ABC中，AC=BC，以AC为直径作⊙O交AB于E，作∠BCA的外角平分线CF交⊙O于F，连接EF．那么EF与BC相等吗？为什么？
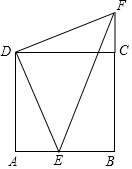已知：如图，E点是正方形ABCD的边AB上一点，AB=4，DE=6，△DAE逆时针旋转后能够与△DCF重合．
完成下列证明过程．
如图所示，在等边三角形ABC中，剪去∠A，∠C后，∠1+∠2+∠3+∠4=480°．