题目内容
4. 如图,在边长为1的正方形ABCD的一边上取一点E,使AE=$\frac{1}{4}$AD,过AB的中点F作HF⊥EC于点H.
如图,在边长为1的正方形ABCD的一边上取一点E,使AE=$\frac{1}{4}$AD,过AB的中点F作HF⊥EC于点H.(1)求证:FH=FA;
(2)求EH:HC的值.
分析 (1)如图所示:连接EF,CF.设正方形的边长为4a,则AE=a,AF=BF=2a.由勾股定理得:EF=$\sqrt{5}a$,FC=2$\sqrt{5}$a,EC=5a.从而可证明△EFC是直角三角形,利用面积法可求得FH=2a,于是得到FH=FA;
(2)在Rt△EFH中,由勾股定理得:HE=a,从而得到HC=4a,故此可求得EH:HC=1:4.
解答 解:(1)如图所示:连接EF,CF.
设正方形的边长为4a,则AE=a,AF=BF=2a.
由勾股定理得:EF=$\sqrt{A{E}^{2}+A{F}^{2}}$=$\sqrt{5}a$,$FC=\sqrt{B{F}^{2}+B{C}^{2}}$=2$\sqrt{5}$a,EC=$\sqrt{D{E}^{2}+D{C}^{2}}$=5a.
∵$(\sqrt{5}a)^{2}$+(2$\sqrt{5}$)2=25a2,
∴EF2+FC2=EC2.
∴△EFC是直角三角形.
∴CE•HF=EF•FC,即$5a•HF=\sqrt{5}a•2\sqrt{5}a$.
解得:FH=2a.
∴FH=FA.
(2)由勾股定理得:HE=$\sqrt{E{F}^{2}-F{H}^{2}}$=a.
∵HC=EC-EH,
∴HC=5a-a=4a.
∴EH:HC=a:4a=1:4.
点评 本题主要考查的是勾股定理和勾股定理的逆定理的应用,利用面积法求得FH的长是解题的关键.

练习册系列答案
相关题目
13.方程(x-2)(x-3)=6的两根分别为( )
| A. | 2或3 | B. | 5或0 | C. | 5或1 | D. | 4或6 |
14.化简(a+1)+a(a+1)+a(a+1)2+…+a(a+1)2015等于( )
| A. | (a+1)2014 | B. | (a+1)2015 | C. | (a+1)2016 | D. | (a+1)2017 |
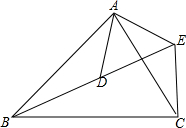 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,请猜想∠BAD与∠CAE的关系,并说明理由.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,请猜想∠BAD与∠CAE的关系,并说明理由.