题目内容
6.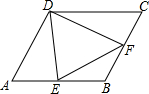 在菱形ABCD中,∠A=60°,E、F分别在AB,BC上,若△DEF有一个角为60°,求证:△DEF一定是等边三角形.
在菱形ABCD中,∠A=60°,E、F分别在AB,BC上,若△DEF有一个角为60°,求证:△DEF一定是等边三角形.
分析 分三种情形讨论:①若∠EDF=60°,只要证明△DAE≌△DBF即可解决问题.②若∠DEF=60°,③若∠DFE=60°,②、③的证明可以转化为证明∠EDF=60°即可.
解答 证明:①若∠EDF=60°,连接BD,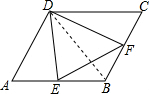 ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴AD=AB.
∵AD=AB,∠A=60°,
∴△ABD为等边三角形.
∴AD=BD,∠ADB=60°.
∵∠ADE+∠EDB=60°,∠FDB+∠EDB=60°,
∴∠ADE=∠FDB.
∵四边形ABCD是菱形,∠A=60°,
∴∠DBF=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×120°=60°.
∴∠DAE=∠DBF.
在△DAE和△DBF中,
$\left\{\begin{array}{l}{∠ADE=∠BDF}\\{AD=BD}\\{∠A=∠DBF}\end{array}\right.$,
∴△DAE≌△DBF(ASA).
∴DE=DF.
又∵∠EDF=60°,
∴△EDF为等边三角形.
②若∠DEF=60°,
∵∠DEF=∠DBC=60°,
∴D、E、B、F四点共圆,
∴∠EDF+∠ABC=180°,
∴∠EDF=60°,
∴由(1)可知△DEF是等边三角形.
③若∠DFE=60°,
∵∠DFE=∠DBE=60°,
∴D、E、B、F四点共圆,
∴∠EDF+∠ABC=180°,
∴∠EDF=60°,
∴由(1)可知△DEF是等边三角形.
点评 本题考查菱形的性质、等边三角形的判定、四点共圆、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,学会转化的思想解决问题,把②、③两种情形转化为①,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.n个连续偶数按规律排成表:
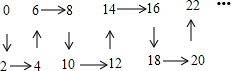
根据规律,从2016到2018,箭头的方向依次应为( )
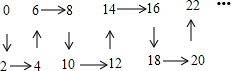
根据规律,从2016到2018,箭头的方向依次应为( )
| A. | ↑→ | B. | →↑ | C. | ↓→ | D. | →↓ |
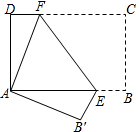 如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.
如图,将矩形纸片ABCD折叠,使点C与点A重合(折痕为EF),剪去不折叠的部分.