题目内容
16.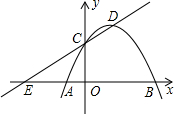 如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.
如图,已知抛物线y=ax2+bx+c(a<0)经过点A(-1,0),B(3,0),且与y轴交于点C,点D为顶点,直线CD与x轴交于点E,以DE为腰作等腰Rt△DEF,若点F落在y轴上时a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.
分析 设交点式得到y=ax2-2ax-3a,则可表示出D(1,-4a),C(0,-3a),再利用待定系数法求出直线CD的解析式为y=-ax-3a可确定E(-3,0),然后分类讨论:当EF=ED时,如图1,过E点作HQ∥y轴,过点C、F分别作x的平行线交HQ于H、Q,通过证明△DEH≌△EFQ得到HE=QF,即-4a=3;当DF=DE时,如图2,作DQ⊥x轴于Q,DH⊥y轴于H,通过证明△DFH≌△DEQ得到DG=DH,即-4a=1,再分别解方程即可得到a的值.
解答 解:设抛物线解析式为y=a(x+1)(x-3)=ax2-2ax-3a,
∵y=a(x-1)2-4a,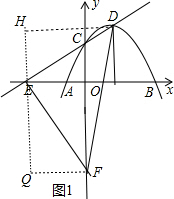
∴D(1,-4a),
当x=0时,y=ax2-2ax-3a=-3a,则C(0,-3a),
设直线CD的解析式为y=kx-3a,
把D(1,-4a)代入得k-3a=-4a,解得k=-a,
∴直线CD的解析式为y=-ax-3a,
当y=0时,-ax-3a=0,解得x=-3,则E(-3,0),
当EF=ED时,如图1,过E点作HQ∥y轴,过点C、F分别作x的平行线交HQ于H、Q,
∵∠DEF=90°,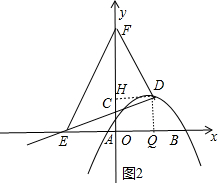
∴∠DEH+∠FEQ=90°,
而∠DEH+∠EDH=90°,
∴∠EDH=∠FEQ,
在△DEH和△EFQ中
$\left\{\begin{array}{l}{∠H=∠Q}\\{∠EDH=∠FEQ}\\{DE=EF}\end{array}\right.$,
∴△DEH≌△EFQ,
∴HE=QF,即-4a=3,解得a=-$\frac{3}{4}$;
当DF=DE时,如图2,作DQ⊥x轴于Q,DH⊥y轴于H,
∵∠DFH+∠DCF=90°,
∠ACE+∠AEC=90°,
而∠ACE=∠DCF,
∴∠AEC=∠DFH,
在△DFH和△DEQ中
$\left\{\begin{array}{l}{∠DHF=∠DQE}\\{∠DFH=∠DEQ}\\{DF=DE}\end{array}\right.$,
∴△DFH≌△DEQ,
∴DG=DH,即-4a=1,
∴a=-$\frac{1}{4}$,
综上所述,a的值为-$\frac{1}{4}$或-$\frac{3}{4}$.
故答案为-$\frac{1}{4}$或-$\frac{3}{4}$.
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).也考查了坐标与图形的性质.解决本题的关键是利用等腰直角三角形的性质构建全等三角形证明线段相等.

| A. | 36.32×108 | B. | 3.632×108 | C. | 3.632×109 | D. | 0.3632×1010 |
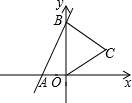 如图,直线y=2x+4与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移4个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )
如图,直线y=2x+4与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移4个单位,使其对应点C′恰好落在直线AB上,则点C的坐标为( )| A. | (5,2) | B. | (4,2) | C. | (3,2) | D. | (-1,2) |
| A. | 1个 | B. | 3个 | C. | 4个 | D. | 5个 |