题目内容
8．先化简，再求值：（$\frac{{x}^{2}-4}{{x}^{2}-4x+4}$-$\frac{x}{{x}^{2}-2x}$）（x-$\frac{4}{x}$），其中x=-$\frac{1}{2}$．分析 先根据分式混合运算的法则把原式进行化简，再把x的值代入进行计算即可．
解答 解：原式=（$\frac{x+2}{x-2}$-$\frac{1}{x-2}$）•$\frac{（x+2）（x-2）}{x}$
=$\frac{x+1}{x-2}$•$\frac{（x+2）（x-2）}{x}$
=$\frac{（x+1）（x+2）}{x}$，
当x=-$\frac{1}{2}$时，原式=$\frac{（-\frac{1}{2}+1）（-\frac{1}{2}+2）}{-\frac{1}{2}}$=-$\frac{3}{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
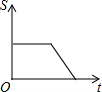
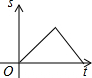
如图所示，AB是半圆O的直径，点P从点A出发，沿A→B→O→A的路径运动一周．设OP为s，运动时间为t，则下列图形能大致地刻画s与t之间关系的是（ ）
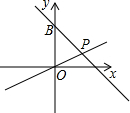如图，一次函数y=-x+m与y轴交于点B，与正比例函数y=$\frac{1}{2}$x的图象交于点P（2，n）．
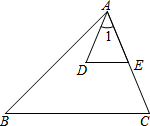如图，在△ABC中，点E是AC上一点，DE∥BC，∠1=∠B，AD=AE．求证：AB=BC．