题目内容
如图,如果AB∥DE,那么∠BCD=( )
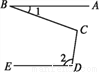
A. ∠2=∠1 B. ∠1+∠2 C. 180°+∠1-∠2 D. 180°+∠2-2∠1
C
【解析】试题分析：过点C作CF∥AB，
∴∠1＝∠BCF，
∵AB∥DE，
∴DE∥CF，
∴∠DCF＝180°－∠2，
∴∠BCD＝∠BCF＋∠DCF＝∠1＋180°－∠2＝180°＋∠1－∠2．
故选：C．
练习册系列答案
相关题目
如图所示，AB，CD，EF交于点O，∠1=20°，∠2=60°，求∠BOC的度数.
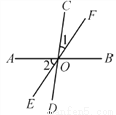
∠BOC=80°.
【解析】试题分析:根据∠2和∠BOF是对顶角,所以∠2=∠BOF,所以∠BOC=∠1+∠BOF=20°+60°=80°.
试题解析:因为∠BOF=∠2=60°,
所以∠BOC=∠1+∠BOF=20°+60°=80°. 如果tanα=0.213，那么锐角α的度数大约为（ ）
A. 8° B. 10° C. 12°
C
【解析】试题分析：使用2nd键，然后按tan-1 0.213即可求出∠α的度数．
∵tanα=0.213，
∴∠α≈12°．
故选C． 在一次实验中，小明把一根弹簧的上端固定、在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体质量x的一组对应值．
所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | 28 |
①上表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？
②当所挂物体重量为3千克时，弹簧多长？不挂重物时呢？
③若所挂重物为7千克时（在允许范围内），你能说出此时的弹簧长度吗？
①上表反映了弹簧长度与所挂物体质量之间的关系；其中所挂物体质量是自变量，弹簧长度是因变量；②当所挂物体重量为3千克时，弹簧长24厘米；当不挂重物时，弹簧长18厘米；③32厘米．
【解析】试题分析：①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量，所以反映了所挂物体的质量和弹簧的长度之间的关系，所挂物体的质量是自变量；弹簧的长度是因变量；
②由表可知，当物体的质量为3kg时，弹簧的长... 如图，在△ABC中，按以下步骤作图：①分别以A、B为圆心，大于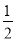
AB的长为半径画弧，相交于两点M，N；②作直线MN交AC于点D，连接BD．若∠A＝25°，则∠CDB＝（ ）
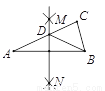
A. 25° B. 90° C. 50° D. 60°
C
【解析】试题解析：由作图的步骤可知，直线MN是线段AB的垂直平分线，
∴DA=DB，
∴∠DBA=∠A=25°，
∴∠CDB=∠DBA+∠A=50°，
故选C． 如图,在△ABC中,AB=AC,AD=BD=BC,则∠A的度数是( )
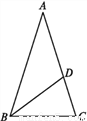
A. 30° B. 36° C. 45° D. 20°
B
【解析】【解析】
设∠A=x°．∵BD=AD，∴∠A=∠ABD=x°，∠BDC=∠A+∠ABD=2x°．
∵BD=BC，∴∠BDC=∠BCD=2x°．
∵AB=AC，∴∠ABC=∠BCD=2x°．
在△ABC中，x+2x+2x=180，解得：x=36，∴∠A=36°．
故选B． 根据不等式的基本性质，求出下列不等式的解集．
(1) 
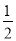x＞－3；
(2)3x－6≤0；
(3)－12x＋6＞0.
(1) x＞－6. (2) x≤2. (3) x＜.
【解析】分析：根据不等式的性质即可求解.
本题解析： (1)两边都乘以2，得x＞－6.
(2)两边都加上6，得3x≤6.两边都除以3，得x≤2.
(3)两边都减去6，得－12x＞－6.两边都除以－12，得x＜. x＜y得到ax＞ay的条件应是____________．
a＜0
【解析】∵x＜y得到ax＞ay是两边同时乘以a，不等号的方向发生了改变，∴a＜0． 如图所示，四边形ABCD中，AE、AF分别是BC、CD的垂直平分线，∠EAF＝80°，∠CBD＝30°，则∠ADC的度数为( )
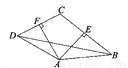
A. 45° B. 60°
C. 80° D. 100°
B
【解析】连接AC，
∵AE、AF分别是BC、CD的垂直平分线，
∴AB=AC=AD，
∵AF⊥DC，AE⊥BC，
∴∠CAF=∠DAF，∠CAE=∠BAE．
∴∠DAB=2∠EAF=160°，
∴∠ABD=（180°-160°）÷2=10°，
∴∠ABC=∠ACB=30°+10°=40°；
在四边形AECF中，
∠FCE=360°-9...