��Ŀ����
��ͼ,�ڡ�ABC��,AB=AC,AD=BD=BC,���A�Ķ�����(��)
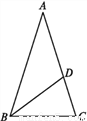
A. 30�� B. 36�� C. 45�� D. 20��
 B
����������������
���A=x�㣮��BD=AD�����A=��ABD=x�㣬��BDC=��A+��ABD=2x�㣮
��BD=BC�����BDC=��BCD=2x�㣮
��AB=AC�����ABC=��BCD=2x�㣮
�ڡ�ABC�У�x+2x+2x=180����ã�x=36�����A=36�㣮
��ѡB��
B
����������������
���A=x�㣮��BD=AD�����A=��ABD=x�㣬��BDC=��A+��ABD=2x�㣮
��BD=BC�����BDC=��BCD=2x�㣮
��AB=AC�����ABC=��BCD=2x�㣮
�ڡ�ABC�У�x+2x+2x=180����ã�x=36�����A=36�㣮
��ѡB��
 ��ǰ����ϵ�д�
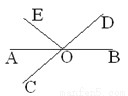
��ǰ����ϵ�д���ͼ����ֱ֪��AB��CD�ཻ�ڵ�O��OAƽ�֡�EOC����EOC=70�㣬���BOD�Ķ�����_______��
 35��
�����������ý�ƽ���ߵĶ���ͶԶ��ǵ����ʼ��㣮
��������
��OAƽ�֡�EOC����EOC=70�㣬
���AOC=35�㣬����ƽ���߶��壩
���BOD=35�㣬���Զ�����ȣ�
����35��
35��
�����������ý�ƽ���ߵĶ���ͶԶ��ǵ����ʼ��㣮
��������
��OAƽ�֡�EOC����EOC=70�㣬
���AOC=35�㣬����ƽ���߶��壩
���BOD=35�㣬���Զ�����ȣ�
����35�� �ÿ�ѧ���������㣬����������ȷ���ǣ�������
A. 175=1419857
B. 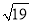 =4.358898944
=4.358898944
C. sin35��=0.573576436
D. ��tan��=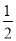 �����=25��56��50��
�����=25��56��50��
 D
��������������������ü������ֱ�����ֻ��D�Ǵ���ģ���Ӧ����26��33��54�壮
��ѡD��
D
��������������������ü������ֱ�����ֻ��D�Ǵ���ģ���Ӧ����26��33��54�壮
��ѡD�� ��(4x2+2x)(x+a)���������в���x2����,��a��ֵΪ_______.
 -
����������������
�����������в���x2�����4a+2=0����a=���ʴ�Ϊ�� ��
-
����������������
�����������в���x2�����4a+2=0����a=���ʴ�Ϊ�� �� ��ͼ,���AB��DE,��ô��BCD=(��)
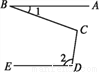
A. ��2=��1 B. ��1+��2 C. 180��+��1-��2 D. 180��+��2-2��1
 C
���������������������C��CF��AB��
���1����BCF��
��AB��DE��
��DE��CF��
���DCF��180�㣭��2��
���BCD����BCF����DCF����1��180�㣭��2��180�㣫��1����2��
��ѡ��C��
C
���������������������C��CF��AB��
���1����BCF��
��AB��DE��
��DE��CF��
���DCF��180�㣭��2��
���BCD����BCF����DCF����1��180�㣭��2��180�㣫��1����2��
��ѡ��C�� ��ͼ��������������ʾ������һ������ʽ�Ľ⼯�� ��
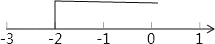
A�� ����1 B��
����1 B�� �ݩ�3 C��x+1�ݩ�1 D����2x��4
�ݩ�3 C��x+1�ݩ�1 D����2x��4
 C
��������
���������������ã������ʾ�Ľ⼯�ǣ�x�ݩ�2���⣾��1�ã�x����2����ݩ�3����x+3�ݩ�6������ʽ�Ľ⼯��x�ݩ�9����x+1�ݩ�1�ã�x�ݩ�2���⩁2x��4��x����2.
��ӦѡC��
C
��������
���������������ã������ʾ�Ľ⼯�ǣ�x�ݩ�2���⣾��1�ã�x����2����ݩ�3����x+3�ݩ�6������ʽ�Ľ⼯��x�ݩ�9����x+1�ݩ�1�ã�x�ݩ�2���⩁2x��4��x����2.
��ӦѡC�� ���в���ʽ�У�������x����1��������
A. 2x��1�ܣ�3 B. 2x��1�ݣ�3
C. ��2x��1��3 D. ��2x��1��3
 A
��������A. �� 2x��1�ܣ�3 ����x��-2�������x����1�����;
B. �� 2x��1�ݣ�3����x��-1���ຬ��x����1�����
C. �ߣ�2x��1��3 ����x��-1���ຬ��x����1�����
D. �ߣ�2x��1��3����x��-2���ຬ��x����1�����
��ѡA.
A
��������A. �� 2x��1�ܣ�3 ����x��-2�������x����1�����;
B. �� 2x��1�ݣ�3����x��-1���ຬ��x����1�����
C. �ߣ�2x��1��3 ����x��-1���ຬ��x����1�����
D. �ߣ�2x��1��3����x��-2���ຬ��x����1�����
��ѡA. ��֪������a��b��c�������ϵ�λ����ͼ��ʾ��������ʽ����ȷ���ǣ� ��
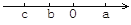
A. cb��ab B. ac��ab C. cb��ab D. c��b��a��b
 A
������������������ȸ���������ص�ó�a��0��b��c���ٸ��ݲ���ʽ�����ʽ����жϣ�
A����a��0��b��c����cb��0��ab. ѡ����ȷ.
B����c��b��a��0����ac��ab. ѡ�����.
C����c��a��b��0����cb��ab. ѡ�����.
D����c��a����c+b��a+b. ѡ�����.
��ѡA��
A
������������������ȸ���������ص�ó�a��0��b��c���ٸ��ݲ���ʽ�����ʽ����жϣ�
A����a��0��b��c����cb��0��ab. ѡ����ȷ.
B����c��b��a��0����ac��ab. ѡ�����.
C����c��a��b��0����cb��ab. ѡ�����.
D����c��a����c+b��a+b. ѡ�����.
��ѡA�� ���߶�AB��CD����AB��CD���ഹֱƽ�֣�����ΪO��AB��2CD���ֱ�ȡOA��OB��OC��OD���е�A�䡢B�䡢C�䡢D�䣬����CA�䡢DA�䡢CB�䡢DB�䡢AC�䡢AD�䡢BC�䡢BD��õ�һ���Ľ���ͼ���������Ľ�����ˮƽ��������ƽ��2���ף�����ƽ��ǰ���ͼ�Σ�
 ������
��������������������ݴ�ֱƽ���ߵ����壬���߶�AB��4���ף�����AB�Ĵ�ֱƽ���߶�CD��2���ף���AB�ڵ�O���ٷֱ�ȡOA��OB��OC��OD���е�A�䡢B�䡢C�䡢D�䣬����CA�䡢DA�䡢CB�䡢DB�䡢AC�䡢AD�䡢BC�䡢BD��õ�һ���Ľ���ͼ��A��B��C��D�䣻�ٸ���ƽ��ͼ�ε����������Ľ���ͼ��A��B��C��D����ĸ�����ֱ�����ƽ��2���ף�����β������㣬���ɵõ��Ľ���ͼ��...
������
��������������������ݴ�ֱƽ���ߵ����壬���߶�AB��4���ף�����AB�Ĵ�ֱƽ���߶�CD��2���ף���AB�ڵ�O���ٷֱ�ȡOA��OB��OC��OD���е�A�䡢B�䡢C�䡢D�䣬����CA�䡢DA�䡢CB�䡢DB�䡢AC�䡢AD�䡢BC�䡢BD��õ�һ���Ľ���ͼ��A��B��C��D�䣻�ٸ���ƽ��ͼ�ε����������Ľ���ͼ��A��B��C��D����ĸ�����ֱ�����ƽ��2���ף�����β������㣬���ɵõ��Ľ���ͼ��... 
