题目内容
在一次实验中,小明把一根弹簧的上端固定、在其下端悬挂物体,下面是测得的弹簧的长度y与所挂物体质量x的一组对应值.
所挂物体质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 18 | 20 | 22 | 24 | 26 | 28 |
①上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
②当所挂物体重量为3千克时,弹簧多长?不挂重物时呢?
③若所挂重物为7千克时(在允许范围内),你能说出此时的弹簧长度吗?
 ①上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;②当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;③32厘米.
【解析】试题分析:①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量,所以反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量;
②由表可知,当物体的质量为3kg时,弹簧的长...
①上表反映了弹簧长度与所挂物体质量之间的关系;其中所挂物体质量是自变量,弹簧长度是因变量;②当所挂物体重量为3千克时,弹簧长24厘米;当不挂重物时,弹簧长18厘米;③32厘米.
【解析】试题分析:①因为表中的数据主要涉及到弹簧的长度和所挂物体的质量,所以反映了所挂物体的质量和弹簧的长度之间的关系,所挂物体的质量是自变量;弹簧的长度是因变量;
②由表可知,当物体的质量为3kg时,弹簧的长...
 阅读快车系列答案
阅读快车系列答案下列尺规作图,能判断AD是△ABC边上的高是( )
A. 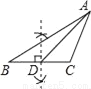 B.
B. 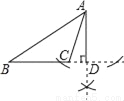 C.
C. 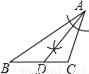 D.
D. 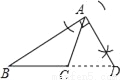
 B
【解析】试题分析:过点A作BC的垂线,垂足为D,故选B.
B
【解析】试题分析:过点A作BC的垂线,垂足为D,故选B. 求满足下列条件的∠A的度数(精确到1″):
(1)cosA=0.8607;
(2)tanA=56.78.
 (1)30°36′18″;(2)88°59′28″
【解析】试题分析:(1)熟练应用计算器,使用2nd键,然后按cos-1 0.8607,即可求出∠A的度数,对计算器给出的结果,用四舍五入法取近似数.
(2)方法同(1).
试题解析:
解:(1)∵cosA=0.8607,
∴∠A≈30.605°=30°36′18″;
(2)∵tanA=56.78,
∴∠A...
(1)30°36′18″;(2)88°59′28″
【解析】试题分析:(1)熟练应用计算器,使用2nd键,然后按cos-1 0.8607,即可求出∠A的度数,对计算器给出的结果,用四舍五入法取近似数.
(2)方法同(1).
试题解析:
解:(1)∵cosA=0.8607,
∴∠A≈30.605°=30°36′18″;
(2)∵tanA=56.78,
∴∠A... 用科学记算器计算,下面结果不正确的是( )
A. 175=1419857
B. 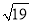 =4.358898944
=4.358898944
C. sin35°=0.573576436
D. 若tanα=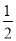 ,则α=25°56′50″
,则α=25°56′50″
 D
【解析】试题分析:利用计算器分别计算后,只有D是错误的,α应等于26°33′54″.
故选D.
D
【解析】试题分析:利用计算器分别计算后,只有D是错误的,α应等于26°33′54″.
故选D. 如果经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
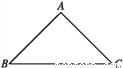
(1)如图,已知等腰直角三角形ABC,∠A=90°,试说明:△ABC是生成三角形;
(2)若等腰三角形DEF有一个内角等于36°,请你画出简图说明△DEF是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)
 (1)见解析;(2)见解析.
【解析】试题分析:(1)根据等腰直角三角形的性质,可得△ABD、△ACD的形状,可得证明结论;
(2)根据顶角是36°,可画底角的角平分线,可得答案,根据顶角是108°的等腰三角形,把顶角分成,可得答案.
试题解析:证明:过点A作AD⊥BC,垂足为D.
∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,∠BAD=∠CAD=∠BAC=45°,...
(1)见解析;(2)见解析.
【解析】试题分析:(1)根据等腰直角三角形的性质,可得△ABD、△ACD的形状,可得证明结论;
(2)根据顶角是36°,可画底角的角平分线,可得答案,根据顶角是108°的等腰三角形,把顶角分成,可得答案.
试题解析:证明:过点A作AD⊥BC,垂足为D.
∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,∠BAD=∠CAD=∠BAC=45°,... 若(4x2+2x)(x+a)的运算结果中不含x2的项,则a的值为_______.
 -
【解析】【解析】
.∵运算结果中不含x2的项,∴4a+2=0,∴a=.故答案为: .
-
【解析】【解析】
.∵运算结果中不含x2的项,∴4a+2=0,∴a=.故答案为: . 如图,如果AB∥DE,那么∠BCD=( )
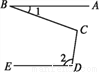
A. ∠2=∠1 B. ∠1+∠2 C. 180°+∠1-∠2 D. 180°+∠2-2∠1
 C
【解析】试题分析:过点C作CF∥AB,
∴∠1=∠BCF,
∵AB∥DE,
∴DE∥CF,
∴∠DCF=180°-∠2,
∴∠BCD=∠BCF+∠DCF=∠1+180°-∠2=180°+∠1-∠2.
故选:C.
C
【解析】试题分析:过点C作CF∥AB,
∴∠1=∠BCF,
∵AB∥DE,
∴DE∥CF,
∴∠DCF=180°-∠2,
∴∠BCD=∠BCF+∠DCF=∠1+180°-∠2=180°+∠1-∠2.
故选:C. 下列不等式中,不含有x=-1这个解的是
A. 2x+1≤-3 B. 2x-1≥-3
C. -2x+1≥3 D. -2x-1≤3
 A
【解析】A. ∵ 2x+1≤-3 ,∴x≤-2,∴不含有x=-1这个解;
B. ∵ 2x-1≥-3,∴x≥-1,∴含有x=-1这个解
C. ∵-2x+1≥3 ,∴x≤-1,∴含有x=-1这个解
D. ∵-2x-1≤3,∴x≥-2,∴含有x=-1这个解
故选A.
A
【解析】A. ∵ 2x+1≤-3 ,∴x≤-2,∴不含有x=-1这个解;
B. ∵ 2x-1≥-3,∴x≥-1,∴含有x=-1这个解
C. ∵-2x+1≥3 ,∴x≤-1,∴含有x=-1这个解
D. ∵-2x-1≤3,∴x≥-2,∴含有x=-1这个解
故选A. 如图,在等边三角形ABC中,∠B、∠C的平分线相交于点O,作BO、CO的垂直平分线分别交BC于点E、F.小明说:“E、F是BC的三等分点.”你同意他的说法吗?请说明理由.
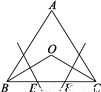
 同意,理由见解析
【解析】试题分析:连接OE、OF,根据等边三角形角平分线的性质,可得∠OBC=∠OCB=30°,由BC的垂直平分线,可知BE=OE,∠EBO=∠EOB=30°,∠OEF=60°,再证,∠OFE=60°,得出△OEF为等边三角形,从而可知EF=OE=BE=OF=FC,得出结论.
试题解析:同意.理由如下:
连接OE、OF,
∵E为BO垂直平分线上的点,且∠O...
同意,理由见解析
【解析】试题分析:连接OE、OF,根据等边三角形角平分线的性质,可得∠OBC=∠OCB=30°,由BC的垂直平分线,可知BE=OE,∠EBO=∠EOB=30°,∠OEF=60°,再证,∠OFE=60°,得出△OEF为等边三角形,从而可知EF=OE=BE=OF=FC,得出结论.
试题解析:同意.理由如下:
连接OE、OF,
∵E为BO垂直平分线上的点,且∠O... 
