题目内容
13.设y=$\frac{2({x}^{2}-1)}{(1-x)^{3}}$÷$\frac{(x+1)^{2}}{(x-1)^{2}}$,先化简,然后确定当x取什么整数时,能使y的值是正整数.分析 首先将原式分解因式,进而化简,再结合整数的定义求出答案.
解答 解:y=$\frac{2({x}^{2}-1)}{(1-x)^{3}}$÷$\frac{(x+1)^{2}}{(x-1)^{2}}$
=$\frac{2(x+1)(x-1)}{-(x-1)^{3}}$×$\frac{(x-1)^{2}}{(x+1)^{2}}$
=-$\frac{2}{x+1}$,
当x=-2时,y=2,当x=-3时,y=1,
即当x取-2或-3时,能使y的值是正整数.
点评 此题主要考查了分式的化简求值,正确分解因式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.将x2+16添加一项,补成一个三项式后恰好是完全平方式,则补上的这个单项式为( )
| A. | 16x | B. | 8x或-8x | C. | 16x或-16x | D. | 8x、-8x或$\frac{1}{64}$x4 |
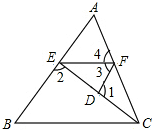 如图,已知∠1+∠2=180°,∠3=∠B,∠4=60°,求∠ACB的度数.
如图,已知∠1+∠2=180°,∠3=∠B,∠4=60°,求∠ACB的度数.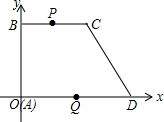 如图.在平面直角坐标系中,梯形ABCD的顶点坐标分别为A(0,0),B(0,8),C(8,8),D(12,0),点P,Q分别从B,D出发以1个单位长度/秒和2个单位长度/秒的速度向C,O出发.设运动时间为t秒(点P到达C点或点Q到达O点,两点均停止运动).
如图.在平面直角坐标系中,梯形ABCD的顶点坐标分别为A(0,0),B(0,8),C(8,8),D(12,0),点P,Q分别从B,D出发以1个单位长度/秒和2个单位长度/秒的速度向C,O出发.设运动时间为t秒(点P到达C点或点Q到达O点,两点均停止运动).