题目内容
18.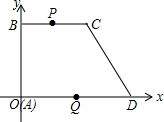 如图.在平面直角坐标系中,梯形ABCD的顶点坐标分别为A(0,0),B(0,8),C(8,8),D(12,0),点P,Q分别从B,D出发以1个单位长度/秒和2个单位长度/秒的速度向C,O出发.设运动时间为t秒(点P到达C点或点Q到达O点,两点均停止运动).
如图.在平面直角坐标系中,梯形ABCD的顶点坐标分别为A(0,0),B(0,8),C(8,8),D(12,0),点P,Q分别从B,D出发以1个单位长度/秒和2个单位长度/秒的速度向C,O出发.设运动时间为t秒(点P到达C点或点Q到达O点,两点均停止运动).(1)写出线段CD的中点坐标(10,4),梯形ABCD的面积为80;
(2)当t为何值时,PC=QD?
分析 (1)作CE⊥OD于E,PF⊥OD于F,利用各点坐标进而得出C点坐标,再利用梯形面积公式求出即可;
(2)由PC=QD得出方程,解方程即可.
解答 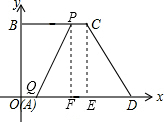 解:(1)作CE⊥OD于E,PF⊥OD于F,如图所示:
解:(1)作CE⊥OD于E,PF⊥OD于F,如图所示:
∵梯形ABCD的坐标为:A(0,0),B(0,8),C(8,8),D(12,0),
∴线段CD的中点坐标为:(10,4),
梯形面积为:$\frac{1}{2}$(BC+OD)×BO═$\frac{1}{2}$(8+12)×8=80;
故答案为:(10,4),80;
(2)∵PC=QD,
∴8-t=2t,
解得:t=$\frac{8}{3}$.
点评 此题主要考查了梯形的性质、坐标与图形性质、梯形面积的计算;熟练掌握坐标与图形性质,由PC=QD得出方程是解决问题(2)的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.乘积(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)…(1-$\frac{1}{201{5}^{2}}$)(1-$\frac{1}{201{6}^{2}}$)等于( )
| A. | $\frac{2014}{2015}$ | B. | $\frac{2015}{2016}$ | C. | $\frac{2015}{4032}$ | D. | $\frac{2017}{4032}$ |
 如图,已知∠A=∠1,∠C=∠D.试说明FD∥BC.
如图,已知∠A=∠1,∠C=∠D.试说明FD∥BC. 如图,在△ABC中,AB=AC=2,∠A=90°,点P为BC的中点,点E、F分别为边AB、AC上的点,若∠EPF=45°,∠FEP=60°,则CF=3-$\sqrt{3}$.
如图,在△ABC中,AB=AC=2,∠A=90°,点P为BC的中点,点E、F分别为边AB、AC上的点,若∠EPF=45°,∠FEP=60°,则CF=3-$\sqrt{3}$.