题目内容
10.已知△ABC∽△DEF,△ABC比△DEF的周长比为1:3,则△ABC与△DEF的面积之比为1:9.分析 根据相似三角形周长的比等于相似比求出相似比,再根据相似三角形面积的比等于相似比的平方解答.
解答 解:∵△ABC∽△DEF,△ABC比△DEF的周长比为1:3,
∴△ABC与△DEF的相似比是1:3,
∴△ABC与△DEF的面积之比为1:9.
故答案为:1:9.
点评 本题考查了相似三角形的性质,熟记性质并确定出相似比是解题的关键.

练习册系列答案
相关题目
5.计算:$\sqrt{3}×\sqrt{6}$的结果是( )
| A. | $9\sqrt{2}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{6}$ |
19.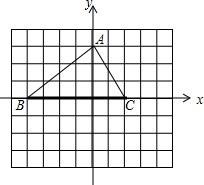 如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )
如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )
 如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )
如图,△ABC的顶点分别为A(0,3),B(-4,0),C(2,0),且△BCD与△ABC全等,则点D坐标可以是( )| A. | (-2,-3) | B. | (2,-3) | C. | (2,3) | D. | (0,3) |
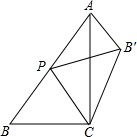 如图,在△ABC中,∠ACB=90°,AB=10,AC=8,P是AB边上的动点(不与点B重合),点B关于直线CP的对称点是B′,连接B′A,则B′A长度的最小值是2.
如图,在△ABC中,∠ACB=90°,AB=10,AC=8,P是AB边上的动点(不与点B重合),点B关于直线CP的对称点是B′,连接B′A,则B′A长度的最小值是2.
 如图,在△ABC中,AB=AC,AD⊥BC,E是AC的中点.若DE=5,则AB的长为10,若AD=8,则BC=12.
如图,在△ABC中,AB=AC,AD⊥BC,E是AC的中点.若DE=5,则AB的长为10,若AD=8,则BC=12.