题目内容
18.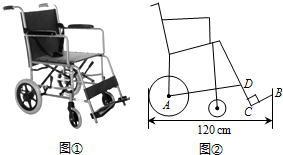 为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:
为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:(1)求横档AD的长;
(2)点C离地面的高度.(sin15°=0.26,cos15°=0.97,精确到1cm)
分析 (1)根据题意结合锐角三角函数关系得出FC,DF的长,进而得出AE的长,再求AD的长;
(2)首先结合锐角三角函数关系得出DE的长,进而表示出点C离地面的高度为:DE+24-DF,即可得出答案.
解答 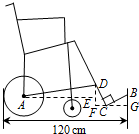 解:(1)如图所示:
解:(1)如图所示:
在Rt△DFC中,FC=DCsin30°=24×$\frac{1}{2}$=12,
DF=DCcos30°=24×$\frac{{\sqrt{3}}}{2}$=$12\sqrt{3}$,
所以CG=DF=$12\sqrt{3}$.
所以AE=120-12-24-12$\sqrt{3}$≈63.2(cm),
在Rt△ADE中,AD=$\frac{AE}{{cos{{15}°}}}$=$\frac{63.2}{0.97}$≈65(cm).
答:横档AD的长为65cm;
(2)在Rt△ADE中,DE=ADsin15°=65×0.26=16.9,
所以点C离地面的高度为:DE+24-DF=16.9+24-$12\sqrt{3}$≈20(cm).
答:点C离地面的高度为20cm.
点评 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
6.下表中是一次函数的自变量x与函数y的部分对应值.
求:(1)一次函数的解析式;(2)求p的值.
| x | -2 | 0 | 1 |
| y | 3 | P | 0 |
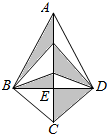 在四边形ABCD中,AC⊥BD于E,且BE=DE,已知AC=10,BD=5,则图中阴影部分的面积=12.5.
在四边形ABCD中,AC⊥BD于E,且BE=DE,已知AC=10,BD=5,则图中阴影部分的面积=12.5.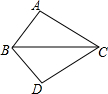 如图所示,把△ABC沿直线BC翻折180°到△DBC,那么△ABC和△DBC是全等图形(填“是”或“不是”);若△ABC的面积为2,那么△BDC的面积为2.
如图所示,把△ABC沿直线BC翻折180°到△DBC,那么△ABC和△DBC是全等图形(填“是”或“不是”);若△ABC的面积为2,那么△BDC的面积为2.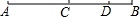 如图,线段AB=8cm,C是AB的中点,点D在CB上,DB=$\frac{3}{8}$CB,则线段CD长是$\frac{5}{2}$cm.
如图,线段AB=8cm,C是AB的中点,点D在CB上,DB=$\frac{3}{8}$CB,则线段CD长是$\frac{5}{2}$cm.