题目内容
7.已知x2+y2=5,xy=1,求x2-y2的值.分析 由题意可知(x+y)2=7,(x-y)2=3,从而可求得x+y与x-y的值,依据平方差公式可知x2-y2=(x+y)(x-y)最后代入求值即可.
解答 解:∵x2+y2=5,xy=1,
∴x2+2xy+y2=7,即:(x+y)2=7.
∴x+y=$±\sqrt{7}$.
∵x2+y2=5,xy=1,
∴x2-2xy+y2=3,即:(x-y)2=3.
∴x-y=$±\sqrt{3}$.
∴x2-y2=(x+y)(x-y)=$±\sqrt{21}$..
点评 本题主要考查的是平方差公式、完全平方公式的应用,熟练掌握平方差公式和完全平方公式是解题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
17.用下列哪种方法解方程3x2=16x最合适( )
| A. | 开平方法 | B. | 配方法 | C. | 因式分解法 | D. | 公式法 |
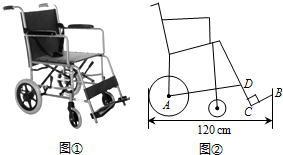 为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求:
为了应对人口老龄化问题,国家大力发展养老事业.某养老机构定制轮椅供行动不便的老人使用.图①是一种型号的手动轮椅实物图,图②为其侧面示意图,该轮椅前后长度为120cm,后轮半径为24cm,CB=CD=24cm,踏板CB与CD垂直,横档AD、踏板CB与地面所成的角分别为15°、30°.求: